Para referências, bibliografia, e demais conteúdos, acesse o livro completo em PDF.
2
ALLOCATIVE EFFICIENCY AND MEASUREMENT OF THE IMPACT OF THE SINGLE TAX
After more than fifteen years of controversy, the debate between those who defend and those who oppose the Single Tax model has produced important conclusions.
As we have shown throughout this text, some of the criticisms have turned out to be mistaken, and others were broadly refuted by facts. Among them are the fears of remonetization of the economy, of flight of depositors from the banking system, of the excessive verticalization of the productive process, of the impossibility of tax exonerations especially for exports, and of worsening the income distribution. At the same time, some of the positive features of bank transaction taxes, such as its imperviousness to tax evasion and its low operational and compliance costs have been widely acknowledged even by the tax’s earlier detractors.
Delfim Netto reflects on these conclusions in an article in which he evaluates the study conducted by the Federal Revenue in defense of the bank debit transactions tax (CPMF). Following a brief summary of what he called “the government’s fiscal/financial philosophy”, he expresses, “certain sympathy with this position, despite finding it nihilistic”. Yet, despite this concession, he immediately criticizes cumulative taxes such as the bank debit transactions tax (CPMF) on an issue which he considers to be the last one not yet properly rebutted by those who defend such taxes. “This discussion avoids the real question of defining what should be the role of fiscal policy in the process of economic development”, and continued, saying, “the productive efficiency of the market economy increases in direct proportion to the decrease in the distortions introduced into relative prices when compared to the free functioning of supply and demand. [...] it is known that cascading taxes introduce greater distortions than value-added taxes.”
Therefore, it is important to evaluate the impact of alternative tax models (cumulative versus VATs) on relative prices.
One of the most important issues in public finance is the normative evaluation of allocative and distributive effects of different systems of taxation. One specific point of interest has to do with comparing the changes in relative-prices introduced by value-added taxes (VAT) to those introduced by turnover taxes, such as the bank transactions tax.
Under highly restrictive conditions, a VAT introduces less relative-price changes than a cumulative tax. For this statement to be true, the following conditions must be met: (a) perfect competition; (b) absence of tax evasion; (c) universal tax base – that is, both taxes must apply to all goods and services transacted in the economy; and (d) a single and identical tax rate applied to both forms of taxation.
The four conditions listed above are very strong assumptions, and none of them is satisfied in the Brazilian economy. The absence of perfect competition is notorious. Large-scale VAT evasion is practiced in a broad variety of forms. Generally, taxation is applied to tax bases that are segmented by sector, activity, or by income categories. And almost all taxes in Brazil have multiple rates.
As such, it is impossible to state, a priori, which form of taxation, VAT or turnover, causes fewer distortions in price determination. With multiple rates, patterns of tax incidence virtually randomized by tax evasion, and sectoral income influenced by varying competitive conditions prevailing in each sector, a definitive statement one way or the other becomes all but impossible.
Thus, it becomes necessary to evaluate empirically the effects these two taxes have on price formation mechanisms.
THE CONSTRUCTION OF THE BRAZILIAN INPUT-OUTPUT TABLE FOR 2006
Input-output economics has proven to be a valuable instrument for investment and development planning. Nevertheless, it has seldom been used in simulating the impact of different tax models on prices.
In this text, an input-output model will be developed to analyze the effects of alternative tax models. The objective is to draw normative conclusions, in terms of equity and allocative efficiency. The simulations will compare value-added to cumulative taxes, such as a bank transactions tax, and will attempt to draw conclusions about their relative advantages and disadvantages in an effort to throw further light in the debate on tax reform in developing countries.
Physical input-output
The system of equations below describes a closed economy with no government, one factor of production (labor), and “n” productive sectors:
X1 = X11 + X12 + X13 + …+ X1n + D1
X2 = X21 + X22 + X23 + …+ X2n + D2
X3 = X31 + X32 + X33 + …+ X3n + D3
.
. (1)
.
Xn = Xn1 + Xn2 + Xn3 + …+ Xnn + Dn
L = L1 + L2 + L3 + ... + Ln
where
i, j = production sectors (1...n)
Xi = gross output of sector i,
Xij = amount of product i used as input by sector j Di = final demand for product i, L = labor inputs in sectors 1…n.
Let aij= Xij/Xj. They show the amount of input i necessary for the production of a unit of output j. Thus, Xij=aijXj, and Xi= aijXj+Di. Thus, in matrix notation, and defining
A= matrix of technical input-output coefficients, with typical elements given by aij= Xij/Xj
it becomes possible to conclude that
X = AX + D
D = (I-A) X
X = (I-A) -1 D (1a)
X = [cij] D
where (I-A) is called the matrix of Leontief Coefficients, and its inverse, (I-A)-1= [cij] is the matrix of direct and indirect requirements of input i for the production of a unit of output j. In order for a sector i to have a positive net production, it is necessary that Xi >Xii and Xi - aii Xi > 0. Thus, aii <1.
Model (1a) is widely used for output and investment planning, since it predicts the correct output combination necessary to produce a projected vector of final demand goods.
Value input-output
The basic physical relationships given by (1) have a dual representation in value terms, where sums of columns and rows are equal:
Y1 = Y11 + Y12 + Y13 + …+ Y1n + D1P1
Y2 = Y21 + Y22 + Y23 + …+ Y2n + D2P2
Y3 = Y31 + Y32 + Y33 + …+ Y3n + D3P3
.
. (2)
.
Yn = Yn1 + Yn2 + Yn3 + …+ Ynn + DnPn W = W1 + W2 + W3 + ... + Wn
Let Yij = Xij Pi , and Yj = Xj Pj. where
Yij = value of sales of sector i to sector j
Pi,j = price of product i, j
Wi = total wage bill paid by sector i.
The value of sales of sector i necessary to produce one unit value of output j is defined as
bij, = Yij/Yj = XijPi/XjPj = Piaij/Pj.
Total wage bill paid by sector j is given by Wj =PL Lj and wj = Wj/Yj = PLLj/PjXj = PLdj/Pj where
PL = price of labor
Lj = total labor input used by sector j dj = Lj/Xj = labor used in a unit production of output j (labor coefficient).
These relationships imply that
Yi = jYij +PiDi = jbijYj + PiDi
which in matrix notation can be expressed as
Y = BY +PD
PD = (I-B)Y (2a)
Y = (I-B)-1 PD
where
Y = value of gross output
B = matrix of input coefficients in value terms
P = vector of product prices
and (I-B)-1 = [I- (Piaij/Pj)]-1 represents the direct and indirect value of product j necessary for the production of a unit value of final demand i.
Model (2a) is also widely used for output and investment planning, and determines the value of production and investment targets, disaggregated by sectors, given a vector of final demand.
Price input-output
Since in value terms sums of rows and of equivalent columns are equal, a typical equation in the system is given by Yi = Yij + Wi . Thus, adding along columns of (2)
Y1 = Y11 + Y21 + Y31 +...+ Yn1 + W1 Y2 = Y12 + Y22 + Y32 +...+ Yn2 + W2 .
.
.
Yn = Y1n + Y2n + Y3n +...+ Ynn + Wn
Since Yi= XiPi and Wi= PLLi, and taking i=1 as a typical equation we get
X1P1 = X11P1 + X21P2 +...Xn1Pn + L1PL (3)
Dividing both sides by X1,
P1 = (X11/X1)P1 + (X21/X1)P2 +...+(Xn1/X1)Pn + L1PL/X1
and remembering that aij=Xij/Xj and that dj = Lj/Xj we get the basic economic identity in production and price formation, without taxation,
P1 = a11P1 + a21P2 +...+an1Pn + d1PL
P2 = a12P1 + a22P2 +...+an2Pn + d2PL
P3 = a13P1 + a23P2 +...+an3Pn + d3PL
.
. (4)
.
Pn = a1nP1 + a2nP2 +...+annPn + dnPL
In matrix notation,
P = A´ P + d PL
P = (I-A´)-1 d PL (5)
where
A´= transpose of A =[aij] d = [di] =vector of labor coefficients.
Model (5), which is a variant of model (2a), allows the simulation of the impact of factor prices (wages in this simple model) on product prices. This is the basic relationship that will be used to analyze the impact of different tax models on product prices.
THE SIMULATION MODEL AND THE STATISTICAL DATA BASE
According to model (5), simulations will require data on the technical inputoutput coefficients aij, as given by the intermediate consumption matrix A.
Brazilian National Accounts are reported in value terms. Thus, it is possible to derive the bij coefficients which express the value of sales of sector i necessary to produce one unit value of output j, as expressed in matrix B. This will be the basis of our simulation models, and the equivalence of matrices A and B for our purposes will be shown below as we need to normalize the price vector to be equal to unity.
In this section, the model to be used in our simulations will be constructed, considering the data availability as given by the official National Income Accounts.
Brazilian National Accounts Tables report the profit margins in each sector.
Thus, such information is incorporated in the model by making equation (3) equal to X1P1 = (X11P1 + X21P2 +...Xn1Pn + L1PL) (1+ m1)
where
m1 = mark-up coefficient on circulating capital.
Since aij=Xij/Xj and dj = Lj/Xj we get
P1 = (a11P1 + a21P2 +...+an1Pn + d1PL) (1 + m1)
P2 = (a12P1 + a22P2 +...+an2Pn + d2PL) (1 + m2)
P3 = (a13P1 + a23P2 +...+an3Pn + d3PL) (1 + m3)
. (6)
.
.
Pn = (a1nP1 + a2nP2 +...+annPn + dnPL) (1 + mn)
In matrix notation,
P = (F0 A´) P + F0d PL , and
P = (I – F0A´) -1 F0 d PL (7)
where
A´= transpose of A =[aij]
F0 = diagonal matrix of mark-up coefficients [1+mi] d = [di] =vector of labor coefficients.
Since, as seen before, aij = Xij/Xj and dj = Lj/Xj algebraic manipulation of a typical row ( such as i=1) of system of equations (6) results in
P1 = [(X11/X1)P1 + (X21/X1)P2 +...+(Xn1/X1)Pn + L1PL/X1] (1 + m1)
Multiplying both sides by (X1/ X1P1) yields
1 = [(P1X11)/ X1P1 + (P2X21)/ X1P1 +...(PnXn1)/X1P1 + + (PLL1)/ X1P1] (1 + m1)
Remembering that each element in the input-output table B is given by bij = (PiXij)/(PjXj), and that wj = (PL Lj)/(PjXj), by substitution we get the basic estimating data used in the simulations, whereby prices are normalised to be equal to one. Thus,
1 = (b11 + b21 + b31 + ...+ bn1 + w1) (1 + m1) 1 = (b12 + b22 + b32 + ...+ bn2 + w2) (1 + m2) 1 = (b13 + b23 + b33 + ...+ bn3 + w3) (1 + m3)
.
. (8)
.
1 = (b1n + b2n + b3n + ...+ bnn + wn) (1 + mn)
An input-output table for 2006 constructed in the format of equation (8) is used in simulating the economic impacts of different taxes. Note that since it is built in a way that forces Pi =1 for all i, and since we know that bij, = Piaij/Pj, then bij must be equal to aij.. Thus, model (8) is equivalent to model (6). In other words, in building our simulation models it is irrelevant which one is actually employed. Thus, in describing the dynamics of the structure of industrial price formation we chose model (6), which is more intuitive as far as price formation and tax simulations are concerned.
The construction of the input-output table
It is necessary to produce a matrix of input-output coefficients representing intermediate use of inputs in production. In terms of value, such information is contained in matrix B, as in model (8), or, in physical units, in its dual matrix A, as in model (6).
Brazilian National Accounts statistics, which follow the guidelines set up by the 1993 United Nations System of National Accounts (1993 SNA), allow the construction of the input-output matrix B for 2006, the latest available year up to the date of this publication.
The starting point for the construction of an input-output table is the Supply and Use tables (SUTs) which are part of the National Accounts Statistics, as published by the IBGE (Brazilian Institute of Geography and Statistics).
The Brazilian SUTs contain production and use (supply and demand) statistics for 110 products and 55 activities. The official Brazilian input-output table is made up of 55 activities. However, as the SUTs contain production information for 110 products, it is possible to construct a 110 entry input-output table organized in terms of products X products, instead of activities X activities. Doing so results in more disaggregated information, which is preferable as it allows more precise analysis of the impact of taxes on prices.
This was done as follows.
SUTs are products X activities matrices that have three parts:
1. The resources table, (also called the “make” table);
2. The intermediate uses table; and 3. The final uses (or final demand) table.
From the SUTs, and assuming that i=row, j= column, that a capital letter represents a matrix, and that a lowercase letter represents a column vector, the following tables can be derived:
where
V= matrix of value of production of each activity, by product, in basic prices;
U = matrix of total intermediate consumption (domestic and imported goods) of each product by activity, in market prices;
M= matrix of margins, taxes and imports, where columns represent respectively a trade margin vector (tm), a transport margin vector (trm), a vector of import taxes (mt), an IPI tax vector (ipi), an ICMS tax vector (icms), and a vector of other taxes net of subsidies (ot);
F = matrix of final demand by type of final demand, where columns represent respectively the vectors of final consumption by families, government consumption, exports, capital formation, and inventory changes; such final demand vectors will be referred to as (Fj), and are all expressed in market prices; m = vector of value of imported products q= vector of gross value of production for each product; and g= vector of gross value of production for each activity.
For illustrative purposes a reduced 12 sector National Account Table is reproduced in ANNEX I-C.
In order to produce an input-output table from the SUTs it is necessary to make important adjustments for two basic reasons: a) because prices in the table of intermediate consumption (U) are reported in market (or consumers´) prices, whereas we wish to have an input-output table in basic (or producers´) prices, and b) because the intermediate consumption table does not differentiate between domestic and imported products, whereas we wish to have an input-output table of domestic production.
The relationship between basic and market prices are given by
Basic Prices = Market Prices – Trade Margin – Transport Margin – (Taxes - Subsidies).
Thus, the first task is to take margins, taxes, and imports out of the values reported in the intermediate use table, and transform them from total intermediate use tables at market prices to intermediate use of domestic products at basic prices. In other words, it is necessary to find dt such that
Unbp = Ump - dt
where
Unbp = matrix of intermediate consumption of domestic goods of each product by activity, and dt = matrix that registers the sum of the value of margins, taxes and imports to be subtracted from the corresponding entry in the U matrix in order to turn it from a market price total intermediate use table at market prices into a basic price table of intermediate consumption of domestic products, by each activity, and bp = basic prices mp = market prices.
Since trade margins, transport margins, and taxes (which are columns of M), and the imports vector in the supply table of the SUT´s are column vectors by products, and therefore do not discriminate by activities, it becomes necessary to adopt a distribution criterion according to which total margins, taxes, and imports are distributed to the activities that produce such products. It should be noticed that even in the construction of a product X product input-output table the margins, taxes, and imports are first distributed among activities, and the resulting intermediate domestic consumption (now in market prices) by activities are allocated to the various production processes and to their secondary production. This two-stage procedure is necessary since the SUTs tables are reported in the product X activities format.
The transformation of market values into basic values, and of total intermediate consumption into domestic intermediate consumption, is obtained through the construction of two distribution matrices (P and P*) used to introduce a weighted average method of distribution of margins, taxes and imports among activities.
Let P be the distribution matrix with a typical cell that represents the value of the intermediate consumption of a product (elements from the U matrix) divided by the value of total demand for the same product, all at market prices as published by the IBGE. Since by construction of the SUTs
q = U.i + F
where
i = column vector where each element has value equal to unity,
it follows that
P = U . <q>-1
where
<a> is a diagonal matrix with elements given by vector a.
A typical element of P is
[uij/ j uij + j Fj]
showing the proportion of a product´s total demand used up as intermediate consumption in each of the activities that produce such a product.
Matrix P can be used to distribute the values of a column vector (such as total trade margin, or total transport margin) used up by the production of a good or service (a product) proportionally to the fraction of the product value which is produced by each activity.
Thus, the allocation of trade margins among the various activities is given by
Ptm = P´. <tm>
where
Ptm = matrix of products´ total trade margin distributed by activities that produce such product, and
P´= transpose of P
The transpose of matrix Ptm, expressed as
P´tm = ( P´.<tm> )´ (9)
has as each of its elements the portion of the of total trade margin to be subtracted from each respective entry in the U matrix.
Similar procedure is used to calculate the matrix
Ptrm = P´. <trm>
where
Ptrm = matrix of products´ total transport margin distributed by activities that produce such product.
Similarly, we can derive
P´trm = ( P´.<trm> )´ (10)
which has in each of its cells the portion of the of total transport margin to be subtracted from each respective entry in the U matrix.
Following the same procedures, the distribution matrix for the IPI tax (ipi) and for Other Taxes Minus Subsidies (ot) are given by
P´ipi = ( P´.<ipi> )´ (11)
P´ot = ( P´.<ot> )´ (12)
The need to construct two distribution matrices (P and P*) is due to the fact that it is necessary to subtract the value of exports (a column of the F matrix) from total final demand when computing the distribution coefficient for some vectors of the final demand, such as Import Taxes, and the ICMS tax. This becomes necessary since none of such taxes are levied on exports, and therefore the value of exports should not influence the weights on the distribution of such taxes, which are levied entirely on domestically consumed products.
Furthermore, since we wish to produce an input-output table for domestic production, it also becomes necessary to subtract the imported components from each element of the U matrix. Thus,
P*= U . <q*> -1
where
q*= U.i + (F-Fx)
and
Fx = vector of value of exports by product.
The “net of exports” distribution matrix P* is used to calculate the value of imports, import taxes and the value of the ICMS tax to be subtracted from each element of the U matrix, following similar procedures as those used with trade and transport margins, and with IPI and Other Taxes. Thus, the required adjustment for the ICMS (icms), for Imports (m) and for Import Taxes (mt) are given by
P*´icms = ( P*´.<icms> )´ (13)
P*´m = ( P*´.<m> )´ (14)
P*´mt = ( P*´.<mt> )´ (15)
Finally, to transform the U matrix from a market price table into a basic price table, and also from a total intermediate use table into a domestic intermediate use table (and remembering that Unbp = Ump – dt ) it suffices to subtract each of the distributed margins, taxes, and imports from each cell in the U matrix, thus transforming it from a market price, total intermediate use table (Ump) into a basic price table of intermediate consumption of domestic products by activities (Unbp).
Thus, the matrix dt is the the sum of the matrices given by equations (9), (10),
(11), (12), (13), (14) and (15) where each equation gives the value of the margins, taxes, and imports that should be subtracted from the respective entry in the U matrix in order to turn it from a market price (Ump) into a basic price table (Unbp).
The resulting Un matrix, at basic prices, is the fundamental component in the development of the input-output models used hereafter.
But before the basic input-output model is constructed a second methodological question must be tackled.
The published official SUTs (more specifically the U matrix from which we derived the Un matrix) are rectangular matrices containing 110 products and 55 activities. The IBGE also publishes a square input-output table with 55 entries by activities. However, as seen before, it is possible to construct a 110 entry inputoutput table organized in terms of products X products, instead of activities X activities.
To do so, we start with a few basic questions and relations.
One question is how to transfer demand for 110 products to the 55 activities; alternatively, how to distribute the output of 55 activities into the 110 production processes.
The second question is how to allocate the intermediate consumption of inputs to the 55 activities; or alternatively to the 110 production processes.
The methodology to deal with the first question implies the construction of a Market Share Matrix D as follows:
D = V . <q>-1
and
V = D . <q> (16)
The market share matrix D will be used to distribute demand from products to activities.
To answer the second question, and to allocate the intermediate demand for domestic products to activities, we assume that inputs are proportional to value of production according to the Matrix of Domestic Technical Input-Output Coefficients at basic prices Bn given by
Bn = Unbp . <g>-1 (17)
from where it follows that
Bn . <g> = Unbp (18)
showing that each intermediate use of a product by an activity is divided by total value of production for that same activity.
Finally, observing the Use Table of the SUTs , it can be seen that the vector representing the value of production by product is given, from the demand or use side, by
q = Unbp . i + Fn (19)
with a typical element in basic prices given by [qi = j unij + Fni], or alternatively, from the supply or resource side of the SUTs,
q = V´. i
where V´is the transpose of V, and with a typical element given by
[qi = j v´ji].
Also, the value of production by activity is given by
g = V.i (20)
with a typical element equal to [gj = i vij].
Total value of production, the sum of columns or of rows, is given by
i qi = j gj .
Substituting equation (18) into equation (19) and eliminating Unbp yields
q = Bn <g>. i + Fn
q = Bn . g + Fn (21)
Next, multiplying both sides of equation (16) by the column vector i , remembering equation (20), and since <q>.i = q
g = D.q (22)
and substituting (22) into (21) yields
q = Bn . D . q + Fn q – Bn. D. q = Fn q (I-Bn.D)-1= Fn
q = (I-Bn.D)-1 Fn (23)
Equation (23) is the basic product X product input-output model used in the simulations that follow.
It is worth noticing that the activity X activity input-output model could be easily obtained by substituting (21) into (22), yielding
g = D.(Bn.g +Fn) g – D.Bn.g = D.Fn g.(I-D.Bn) = D.Fn
g = (I-D.Bn)-1 D.Fn (24)
Equations (23) and (24) are therefore the two possible representations of the input-output model given the SUTs tables reported for the Brazilian economy, and both are strictly compatible with equation (2a) above, which defines conceptually the input-output model as created by Wassily Leontief. Pre-multiplying the Bn matrix by D (D.Bn) yields the matrix of technical coefficients activity X activity; postmultiplying the Bn matrix by D (Bn.D) yields the matrix of technical coefficients product X product; D.Fn yields final demand vector by activity; and Fn is the final demand vector by product.
After constructing matrix Bn.D, which is what interests us in our simulations, and remembering that prices of all products were constrained to be equal to unity, the matrix of technical coefficients Bn.D is complemented with the following rows: a Sum row, with sums of technical coefficients by column, an Imports row containing the sum by column of the technical coefficients of imported intermediate products, a Wages row, containing coefficients given by the division of the “wages paid” by the “gross value of production” both contained in the value-added part of the Use Table of the SUTs , and finally a residual Gross Profit Margin row, by activity.
Of course, summing the column of intermediate use and adding the value-added components of the production process amounts to unity.
Simulation models
The SIM (0) model
We now construct our simulation models, which will incorporate the basic conceptual input-output model given by (6) together with the empirical matrix of domestic technical input-output coefficients at basic prices (BnD) contained in equation (23).
Equation (6) incorporates information on profit margins through the use of mark-up coefficients applied on circulating capital. We adopt the hypothesis that advances on purchase of inputs and on payment of wages have to wait for a certain production period before it is recovered through sales to other sectors and to final demand. During this period the firms earn a “waiting fee” of mi % of the circulating capital used in purchasing inputs and in paying wages. Such mark-up margin may also include a competitive profit margin, or normal profits. This model is certainly more realistic than the zero-profit assumption implied by (4). Thus, remembering that equation (6) is equivalent to equation (8) (since, as seen before, aij = bij) a typical price accounting equation is given by
Pi = [ j(bijPj) + wi ] (1 + mi )
where
Pi,j = price of product i, j , (1...n) bij = value of input j per unit value of product i wi = value of labor input per unit value of product i mi = mark-up on circulating capital of product i.
In matrix notation the model described above can be expressed as
P=[ F*K ] P + F*w
P- [F*K] P = F*w
[I – F*K] P = F*w
P= [I – F*K]-1 F*w SIM (0)
where
P =vector of final prices (n x 1)
I = identity matrix (n x n)
F* = diagonal matrix [(1 + mi)] (n x n)
K = the transpose of matrix B of technical coefficients bij (n x n) w = vector of wi , value of labor input per unit value of product i (n x 1).
This model, called SIM (0) is the benchmark with which all other simulations will be compared. It represents an economy without taxation, and in which all prices are normalised to equal unity. Note that, in terms of the statistical data available, matrix K above is the exact equivalent to the transpose of matrix (Bn.D) in equation (23). Thus, for strictly denominational purposes K= (BnD)´ in this and in all other variants of the simulation models, as described below.
The introduction of taxation will result in a different set of prices which, compared to unit prices implied by the SIM (0) model, will describe their percentage change resulting from the choice of taxes used by the government. Different taxes will be introduced, and the resulting prices will be compared to those given by the benchmark model (SIM 0) with no taxation.
The SIM (1) model:
This model introduces the bank transactions tax. It is charged on both debit and credit entries on clients´ bank accounts. It has a double incidence on each transaction, shared by purchaser and seller. As an example, suppose that the bank transaction tax with a 1% rate is applied on a $100 purchase of an input for production of a certain output. The purchaser’s bank account will be charged $101, and the sellers bank account will be credited $99. Thus, a $100 transaction will result in tax revenue of $2, shared between the two agents involved in the transaction.
For each economic agent such as a producer, the cost accounting records will register a 1% tax cost on all outlays on inputs and on labor, and also another 1% tax on sales of final products. This can be expressed in terms of prices as
Pi = (1+t) {(1+t)[ j(bijPj) + wi ] (1 + mi )}
where
t = the bank transaction tax rate.
In matrix notation,
P = F[KP + w]
P = [FK]P + Fw
P = [I – FK]-1[Fw] SIM (1)
where
F = diagonal matrix [(1+t)2 (1+mi)]
The SIM (1) model estimates the effect on sector prices of a bank transactions tax. The matrix F, is the product of two diagonal matrices: the first [(1+t)2] , represents the effect of the uniform rate of the bank transaction tax, and the second, [1+mi] reflects the impacts of the sector mark-up coefficients. Matrix F introduces the turnover effect into the system, iterating with the mark-up coefficients.
The SIM (1) model implies that no other tax is imposed, and therefore it isolates the effect of the bank transactions tax on prices. If compared to the hypothetical “no tax” situation implied by the SIM (0) model, the total cumulative effect of a bank transactions tax on sector prices can be effectively evaluated.
The SIM (2) model:
This model introduces a value-added tax into the initial no-tax system SIM (0). As usual, tax payments included in the price of purchased inputs will be deducted from tax liabilities due by the seller of the final product. It is assumed that the final price for each sector comprises the VAT cost according to the following relation:
Pi = [total outlays plus profit margin]/(1-v)
where
v = uniform VAT rate.
Thus, the pricing model can be expressed as
Pi = (1/(1-v)){ [( j(bijPj) + wi ) (1 +mi)] - v j(bijPj)}
or,
Pi = [((1+mi–v)/(1-v)) j bijPj] + ((1 +mi)/(1-v)) wi
In matrix notation the model can be expressed as
P = [F1K]P + F2w
P = (I - F1K)-1 F2w SIM (2)
where
F1 = diagonal matrix [(1+mi-v)/(1-v)]
F2 = diagonal matrix [(1+mi)/(1-v)]
Defining M as the mark-up diagonal matrix with elements [1+mi], A as the VAT diagonal matrix with elements [1/(1-v)], and C as the value-added credit diagonal matrix with elements [-v/(1-v)] it can be seen that F2 = MA and F1 = F2 + C.
It is important to note that in this model the mark-up rate is levied on input prices with the VAT tax included, in the same way as with any other cost of production. Thus, it is assumed that VAT taxes included in input prices are paid as an advance to the government, and that there is a waiting time equivalent to an average production period before the tax advance is paid back to the producer in the form of a credit against his VAT tax liabilities due when final product is sold.
This hypothesis implies that the VAT incidence on final prices is not uniform and cumulative, as opposed by standard theoretical analysis of the incidence of value-added taxation on final prices. VAT´s may have differential impacts on prices of different products, thereby distorting relative prices of intermediate goods in a way that is formally quite similar to cumulative taxes.
It becomes clear, therefore, that the alleged neutrality of the VAT can only be guaranteed in the unlikely situation where all mi= 0, in addition to the seldom seen application of a single VAT tax rate for all products and services traded.
Thus, the assumption that VATs have a neutral impact on relative prices is not warranted, and proves erroneous the assumption that they are less distortionary than turnover taxes as far as their effects on prices are concerned.
The SIM (2´) model:
In a mark-up model, a VAT will show the neutrality properties usually assumed in simplified textbook models, only if it meets an exceedingly strong assumption: that value-added tax credits are instantaneous. In other words, the pricing model becomes
Pi = (1/(1-v)){ [( j(bijPj) + wi ) - v j(bijPj) ] (1 +mi) }
Pi = (1/(1-v)){ [ (1-v) j(bijPj) + wi ] (1 +mi) }
and
Pi = (1 +mi) j(bijPj) + (1+mi)/(1-v) wi
In matrix notation,
P = MKP + F2w
P = (I-MK)-1 F2w SIM(2´)
where
M= the mark-up diagonal matrix with elements [1+mi]
F2 = diagonal matrix [(1+mi)/(1-v)]
It should be pointed out that in this model the prices of intermediate inputs are multiplied by matrix M, composed solely of the mark-up coefficients. Thus, the value-added tax will not influence prices through their effect on prices of intermediate inputs, as happened in model SIM (2) when intermediate prices were multiplied by the F1 matrix, which includes both the mark-up coefficients mi and the value-added tax rate v.
Furthermore, it should be noted that even if mark-up rates equal zero in all sectors, the expected “neutrality” of value-added taxes (defined loosely here as a proportional increase in all prices of intermediate inputs), will only occur if there is a uniform VAT rate applied to all sectors. The multiplicity of value-added tax rates, as is the case in practical applications of such taxes throughout the world, does not guarantee its neutrality, as commonly claimed, even in the (unlikely) case of zero mark-up rates.
On the other hand, the labor cost, which by definition is the same as the valueadded in production, is amplified by the mark-up margin and by the VAT rate v, present in the F2 matrix. The incidence of the VAT on the labor component in production does not allow for credits, since its total incidence falls completely on final prices, as expected by conventional value-added tax theory. Thus, its effects are similar to a tax on final sales, guaranteeing neutrality in intermediate prices, and therefore on production costs. Nevertheless, the assumptions of such model are extremely unrealistic, restricting severely the usefulness of its policy prescriptions.
SIM(2)EXT: extensions of the SIM(2) model
Given the exceedingly strong assumptions implied by the SIM (2´) model, the original SIM (2) structure will be used for comparing alternative tax systems.
Such construct can easily incorporate other taxes in its analytical framework.
Three other important taxes in current use in Brazil can be easily included into that same input-output framework, namely a turnover tax on services, the ISS, a value-added tax on industrial products (IPI, similar to a value-added excise) and the payroll social contribution to the INSS, the federal social security agency.
The incidence of the ISS is upon the value of both intermediate and final gross sales of services. It has an identical impact on prices as the mark-up rate, and thus it suffices to add the sectoral ISS rates to each corresponding mark-up rate, simply adding each si (the ISS rate applicable to sector i ) to each mi. Identical procedure, mutatis mutantis, should be used to introduce the IPI in the model, adding its rate pi to the sectoral VAT rate vi.
As far as the INSS is concerned, its impact on prices is equivalent to an additional labor cost corresponding to the INSS uniform rate µ. Thus, it suffices to replace each wi for w´i, where w´í = (1+µ). Therefore, the simulation model used to represent the conventional Brazilian tax model made up of two value-added taxes, a turnover services tax, and a single social contribution rate on wages can be represented as
Pi = (1/(1-vi´)){ [( j(bijPj) + w´i ) (1 +mi +si)] -
- vi´ j(bijPj)}
where
si= the ISS rate for sector i vi´= v + pi pi = the IPI rate for sector i
w´í = wi(1+µ) µ = the social security rate on wages.
As a result, in the extended SIM(2)EXT model
F1 = diagonal matrix [(1+mi+si –vi´)/(1-vi´)] F2 = diagonal matrix [(1+mi+si)/(1-vi´)] w´ = vector of w´i , value of labor units per unit of product i , including social
contributions.
The simulations contained in this text, therefore, will use the SIM(0) model as the benchmark for a “no tax” situation, which theoretically represents the least distortionary situation, and against which the effects of alternative taxation systems will be compared. The effects of the bank transactions tax on prices will be measured by comparing SIM(1) results against SIM(0). And the SIM(2) model, and its extensions as in the SIM(2)EXT model, will be used to evaluate the current tax system applied in Brazil, as compared with the least distortionary situation implied by model SIM(0).
Evidently, the comparison of both the SIM (1) and the SIM (2) models with the benchmark SIM(0) model, will imply a corresponding comparison of models SIM(1) and SIM(2), as far as their impact on prices are concerned. Thus, the debate between the supporters of a VAT tax and those in favor of a bank transactions’ tax will finally occur with a quantitative perspective in sight, as opposed to the predominantly loose and fragile conceptual framework in which it has been occurring in the last two decades.
SETTING RATES FOR THE SINGLE TAX
The electronic tax on bank transactions was introduced in Brazil in 1993 through the enactment of Article 2 of Constitutional Amendment 3, which authorized a Complementary Law to create a Provisional Tax on Financial Transactions (IPMF). It should be effective until December 31, 1994, with a rate of 0.25% (a quarter of 1%) levied on the value of all current account bank debt entries.
The use of the IPMF, which began to be collected in August 26, 1993, was suspended by a Judiciary order on September 15, 1993 (Adin 939-7/DF). It became effective again on January 1, 1994, and was in force until December 31 of the same year, collecting R$ 3.7 billion, which amounted to 5.17% of total federal revenue, and 1.06% of Brazilian GNP.
Constitutional Amendment 12/96 reintroduced the financial transactions tax under the name of Provisional Contribution on Financial Transactions (CPMF), with a rate of 0.20%. Law 9311/96 authorized its use from January 23, 1997 until February 23, 1998.
From this period onwards a series of time extensions of the CPMF were enacted. The rate was changed in certain short periods, but it remained at 0.38% from 2001 until its extinction in December 31, 2007. The rates of the CPMF were the following:
• 0.20% between January 23, 1997 and January 22, 1999;
• 0.38% between June 17, 1999 and June 16, 2000;
• 0.30% between June17, 2000 and March 17, 2001; and
• 0.38% between March 18, 2001 and December 31, 2007.
TABLE 6 below shows the IPMF/CPMF revenue between 1994 and 2008. Revenue collected in 1995/1996 and 2008, when the financial transactions tax was not in effect, is attributed to residual revenue from taxable transactions which occurred in 1994 and 2007 respectively.
TABLE 6
In the six years during which the full rate of 0.38% was applied, the financial transactions tax collected on average 1.37% of GNP, or 6% of total federal revenue.
Its tax base amounted to 3.6 times the Brazilian GNP.
The Brazilian Tax Burden (2007/2008)
Even without the CPMF, total tax burden in 2008 was 1.15 percentage point above that of the year before, maintaining the upward trend initiated in the early 1990’s. Between 1995 and 2008 total tax burden, including federal, state, and municipal revenues, grew 7.5 percentage points, going from 28.4% to 35.9% of GNP.
To compensate for the projected loss of revenue in 2008 resulting from the cancellation of the CPMF, the rate of the pre-existing tax on loans and credit (IOF) was raised by 0.38%, and that of the Social Contribution on Net Profits (CSLL) of the financial sector was raised from 9% to 15%. Such measures resulted in additional revenue of R$ 23.6 billion in 2008.
TABLE 7 below shows federal and social security revenues for 2007 and 2008, as well as state and municipal fiscal revenues.
TABLE 7
In addition to the effects of higher tax rates on the IOF and on the CSLL for the financial sector, revenue from these taxes increased significantly due to higher volumes of credit transactions and also to higher corporate profits. In 2008, the IOF collected a larger share of GNP than in the previous year (+ 0.4 percentage point), while the CSLL showed a growth of 0.25 percentage point.
Other federal taxes that showed significant revenue growth were the corporate income tax, the withheld income tax on labor income, the international trade tax, and the industrial tax on imports (IPI). Such performance was due to larger corporate profits, to growth in formal employment, and to larger value of imports.
Social Security taxes showed a slight decrease due to the discontinuation of the CPMF, although the loss of revenue was almost completely compensated by the larger revenue raised by the Cofins, the CSLL, and by other social security contributions.
The satisfactory performance of the Brazilian economy in recent years also contributed to the larger state and municipal revenues, such as the ICMS, the ISS and the IPVA.
Single Tax: Estimating the Required Rate
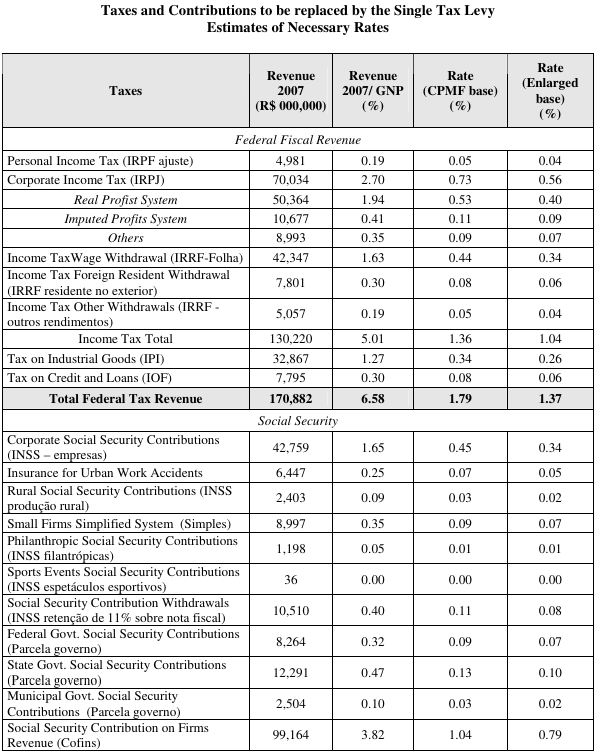
In 2002 the Brazilian tax burden reached 31.86% of GNP. The rate of the Single Tax on Financial Transactions necessary to raise the equivalent revenue was estimated at 5.3%, equally split between the value of banks’ debits and credits.
According to a paper issued by the Federal Revenue Agency named “Brazilian Tax Burden- 2007”, the tax burden in 2007 reached 34.79% of GNP. Together with information issued by another of its various papers called “Analysis of Federal Revenue” published in 2008, and also with data from the “2007 Social Security Statistical Yearbook” we estimate that the rate necessary for the Single Tax to replace in 2007 the same revenue raised in 2002 would be 5.62%. While the tax burden increased 2.93 percentage points during those five years, the Single Tax rate would have to increase by 0.32 percentage point. Thus, for each percentage point increase in the tax burden, the single tax rate would have to be raised by 0.11 percentage point.
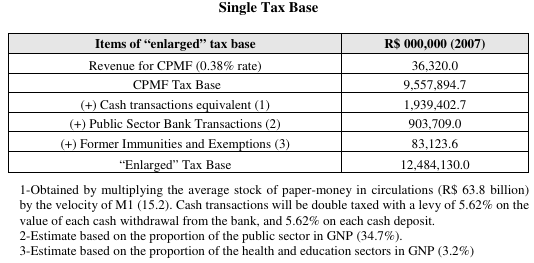
The estimates for the Single Tax rate necessary to replace the revenue raised by all predominantly fiscal taxes are shown in TABLE 8 below, and were based on the performance on the CPMF in 2007, the last year it was collected. We estimated an “enlarged” tax base, which in addition to the conventional CPMF tax base, includes the double taxation of the bank cash withdrawals and deposits, and the Single Tax levying on bank transactions done by the government and by privileged sectors and institutions, constitutionally exempt from the CPMF until 2007.
TABLE 8 below shows the “enlarged” tax base for the Single Tax. The starting point for the estimates is the tax base of R$ 9.6 billion for the CPMF in 2007.
TABLE 8
Total tax revenues to be replaced by the Single Tax collection amounted to 27% of GNP in 2007. Considering the CPMF tax base, federal taxes and contributions amounted to 17.9% of GNP, state revenues to 7.83%, and municipal taxes to another 1.27% of GNP, as can be seen in TABLE 9 below.
To replace all federal fiscal revenue the Single Tax rate would have to be 1.79% according to the CPMF base, and 1.37% according to the enlarged base. Including social security and economic contributions the rates would be respectively 4.87% and 3.72%. Adding the three state taxes and the three municipal taxes, the rate would have to be 7.34% according to the CPMF base, and 5.62% using the enlarged base.
In the Single Tax model, all corporate social contributions to the INSS, to the various quasi-governmental agencies (Sistema “S”), and to the educational fund (FNDE) would be discontinued. Of the approximately 35% of payrolls paid out by firms for social security contributions, only 8% for the Workers Unmotivated Dismissal Compensation Fund (FGTS) would remain.
It should be pointed out that the revenues of the “S”system would continue to be transferred to its administrators. The only change would be the way such revenue is raised. Instead of burdening firms’ payrolls with rates varying from 0.3% to 2.5%, as happened in 2007, it would be raised by the specific rate of 0.05% on bank transactions, which compose the estimated total Single Tax rate of 5.62%. The same would happen to the Education Fund (salário-educação), which instead of being financed by a 2.5% levy on payrolls, would be maintained by a specific rate of 0.06% on bank transactions.
The Single Tax system would imply a significant decrease in the tax load of the productive sector as a result of abolishing taxes on corporate income, on gross revenues, on sales and on profits. Furthermore, administrative costs would be significantly reduced as the costly declaratory taxes would no longer be collected.
Individuals would benefit from an increase in purchasing power as a result of lower indirect taxes on prices, and from a dramatic reduction in individual taxes on wages and on property.
TABLE 9
When the IPMF was introduced in 1993, following the polemical proposal in 1990 for the creation of a Single Tax on Financial Transactions, certain technical requirements for the proper use of a bank transactions tax were ignored by the government. Among them is the inadequacy of its application on transactions in the financial and capital markets. Taxation should not occur as the value of the principal in a capital or financial transaction is registered as credit or debit in a bank account. Taxation should occur only as the flow of real returns of such financial transactions goes through the banking system. Such characteristic of the bank transaction tax was thoroughly discussed elsewhere in this text.
In October 2004 the “investment current account”, linked to its respective bank “current account”counterpart, was created by the Brazilian Central Bank to redress this technical imperfection. The intention was to avoid taxing the value of the stock of financial capital as it flows within the banking system. Taxation of bank debits and deposits would occur only once as the value of the financial investment was transferred to the “investment account”, from where it could circulate, free of taxation, to and from other “investment accounts” to carry out typical financial dealings, such as purchasing and selling of bills, stocks, or any other financial asset.
It was a significant improvement, although in the pure Single Tax model the first transfer of investment funds, as well as all the other subsequent transfers, would be free of taxation as long as it remained within the realm of “investment accounts”. In fact, taxation of transactions in the financial and capital markets would remain very similar to the current income tax on financial returns.
TABLE 10 below shows the income tax revenue on financial profits in 2007, amounting to 1.15% of GNP.
TABLE 10
In the Single Tax model various existing taxes would remain in place, as they are considered to have preponderantly non-fiscal characteristics and are used mainly as instruments in public policy. Such is the case, for instance with the international trade taxes, which are instruments of industrial policy; the rural land tax (ITR), an instrument of land reform policy; and service fees, which are retributions to services rendered to individuals, devoid of the essential characteristics of public goods.
Other levies which would continue to be charged are those that may be considered as negotiated gains for workers, such as compulsory savings or compensatory payments in their favor, such as the Social Integration Fund (PIS), the Compensatory Fund for Unmotivated Dismissals (FGTS), and the own social security contributions of employees.
TABLE 11 below lists taxes, contributions, tax debt payments, fines and compulsory savings collected in 2007 and that would continue to exist even if the Single Tax Model were fully applied.
TABLE 11
SIMULATION RESULTS
The effect of types of different types of taxes on relative-prices can be evaluated using inter-industrial relations (input-output) models described above. We intend to compare the price effects of the Bank Transactions Single-Tax model to those of a VAT using Brazil’s inter-industrial structure drawn from technical coefficients of production contained in a 110 sector input-output table for 2006, constructed from data published by the IBGE [Brazilian Institute of Geography and Statistics].
Model SIM(1), described above, simulates sector prices by applying a singlerate turnover transactions tax, as estimated in the section above. In this model, all sectors have an infinite number of links in their production chains (which contradicts the general belief in the existence of “shorter” or “longer” production chains). The effect of a turnover tax on prices is inversely related to the proportion of value-added relative to the value of inputs from other sectors in each link of the production process. Clearly, the tax effect on final prices resulting from the use of such taxes is as smaller as the greater is the distance that separates a certain production process from the final step where it reaches the final consumer. In the simulations, we use a “mark-up model” to determine profit margins, as found by IBGE’s input-output matrix.
In the simulations, Model SIM(1) was used to evaluate the effect on final prices of the bank transaction tax as the single tax [Single Transaction Tax].
Model SIM(2) was used to evaluate the effect of the pure VAT. To define profit margins, we chose a variation of the “mark-up model” which seems more realistic in the sense of applying the mark-up multiplier to circulating capital as well as to cost of inputs. It is worth stating that no financial costs were imputed to the time spent “waiting” for the use of the tax credits, thus reducing the impact of a VAT on final prices.
It is important to note that we chose not to use Model SIM(2’) as the basis for our simulations, although it is the model that incorporates the conventional assumptions incorporated in the orthodox framework of value-added tax doctrine. The reason, as stated above, is the absurdly unrealistic assumptions that they assume, particularly with respect to developing countries such as Brazil.
Finally, in order to incorporate into the simulation models the other taxes composing the Brazilian tax structure (INSS, IPI, and the ISS) the SIM(2)EXT model was used, as shown above.
In the earliest papers on the Single Tax we sought to evaluate the impact of cumulative taxes on price formation in the economy. Simulations using the IBGE input-output matrices of inter-industrial flows and their updates led to the conclusion that because bank transaction taxes require nominal tax rates that are significantly lower than VAT rates for a given revenue target, and since they, consequently, discourage tax evasion, the bank transaction tax would have less of an impact on relative prices taking an ideal tax-free market equilibrium as a benchmark.
The statistical data and the assumptions implied in the construction of the inputoutput model used in the simulations are summarized in ANNEX I.
Cumulativeness, or the cascading effect, has caused critics to erroneously believe that more roundabout methods of production could drive tax costs upward. Simulations proved that those assertions were mistaken. For example, studies on the
Alternative Proposal demonstrated that the effect of a 2.7% rate bank transaction tax on sector prices ranged from 4.1% to 11.1% price hikes. Greater impact on production costs would be caused by a VAT, such as the ICMS, with 17% rate, bringing the tax burden to between 18.4% and 31.4% of the final price of products. Other studies that have been mentioned earlier used the same methodology and arrived at similar conclusions.
But, despite the absolute impact of a bank transaction tax on prices being weaker than those caused by VATs (assuming a given a revenue target), there remains doubt about the impact on relative prices, as Delfim Netto suspects.
Before trying to measure the impacts of different tax systems on relative prices,
it is worth noticing that there are theoretical reasons to believe that bank transaction taxes will be less distortionary than value-added taxes.
Yitzhaki has suggested that “in the extreme case where all commodities are taxed, they can all be taxed at the same rate, so that relative prices do not change and we end up with a zero deadweight loss.” Thus, a tax system with lower rates, and more widespread universal incidence across all commodities should imply a smaller impact on relative prices, and therefore, have smaller substitution effects and cause less allocative distortions on the economy.
There are two reasons for expecting that bank transaction taxes conform more closely to these requirements of absolute generality stated by Yitzhaki. First, bank transaction taxes have a single uniform rate, universally applied to all commodities. VATs, on the other hand, usually have multiple rates. Second, rates of bank transaction taxes are lower than those required from VATs to achieve a given revenue target: the tax base is broader, and evasion potential is more limited. Thus, it is expected that bank transaction taxes imply lower and more homogeneous tax burdens on commodity prices than VATs, thus being closer to a situation of relative price neutrality, as stated by Yitzhaki.
The simulations results described below confirm these effects.
No doubt, all taxes distort relative prices. However, it is believed that the cumulative effect of a bank transactions tax would cause even more intense distortions. It is believed that the VATs would be less distortionary because the tax burden on final prices could theoretically be determined entirely by economic policymakers and tax legislators as they set nominal tax rates.
The conclusion about the superiority of VATs in commodity production, as against cumulative taxes, would be partially true if two conditions were met: first, absence of tax evasion, and second, the existence of uniform rates for all sectors and products. Given that neither of these conditions is satisfied in real life, the conclusion that VATs necessarily introduce fewer distortions than a bank transactions tax cannot be reached a priori.
The efficiency advantages of VAT´s are highly questionable. The use of multiple rates, proliferation of exemptions, administrative and operational costs, sub national competence to apply value-added taxation and many other empirical shortcomings in the application of the VAT make its practical results fall significantly short of what is expected from its theoretical conclusions. Such problems are especially serious when the VAT is under sub national administration in federative countries
Furthermore, impacts on relative prices are not a result of the type of tax alone, but also of the intensity of the tax’s use, or of the value of its respective rates. Given that, for a specific amount of revenue, the bank transactions tax require rates that are significantly lower than what VATs require, we can immediately notice the fragility of assertions that cumulative taxes must necessarily introduce stronger distortions in relative prices.
The use of multiple rates and the existence of significantly more tax evasion in VATs make its impacts on relative prices be just as uncontrollable, random, and unintentional as they can be for bank transactions taxes.
It is possible that VAT-driven distortions could be even stronger than those generated by a bank transactions tax, given that tax evasion is a highly volatile, mutable, unpredictable, and camouflaged practice. In bank transactions taxes the variability of impacts on sector production costs over time are the result of changes in the production functions, which only occur over the medium and long terms. This means that bank transactions taxes, even with unintentional and uncontrollable patterns of incidence due to its cumulative effect, seem to be more stable than VATs. Tax evasion is generally most unstable even in the very short run, making the allocative effects of VATs a random event, with effects on relative prices even more unpredictable than those caused by a bank transactions tax. The simulations below will attempt to show that:
1. Even assuming away the existing differences in potential tax evasion, a bank transactions tax introduces less allocative distortions than VATs because it requires lower nominal tax rates for a given revenue target;
2. With the possibility of tax evasion being greater for VATs, the effect of these taxes on price becomes strongly distortionary, far exceeding the distortions in relative prices caused by bank transactions taxes.
This is an exercise in comparative statics, in which the tax models of the cumulative bank transaction tax and the non-cumulative VAT will both be compared to a heuristic situation of absence of taxation, which supposedly would be the optimal competitive equilibrium. Therefore, the farther the sector prices cum taxes distance themselves from prices that are free of taxes (which in the model below were set to equal to one, to unit), the greater the distortionary effect that they may have caused on prices, and therefore on tax burden.
The assumptions implied in each of the simulations are detailed in ANNEX I-A. Next, for each simulated situation, a matrix of relative prices shall be constructed (each element being a relative price for a pair of sectors), and the distance of each relative price from the unit value will measure the distortion caused by the respective tax model on the relative prices of that specific pair of sectors. The extent of overall distortion is given by the standard deviation of relative prices of the matrix, relative to the unit relative prices.
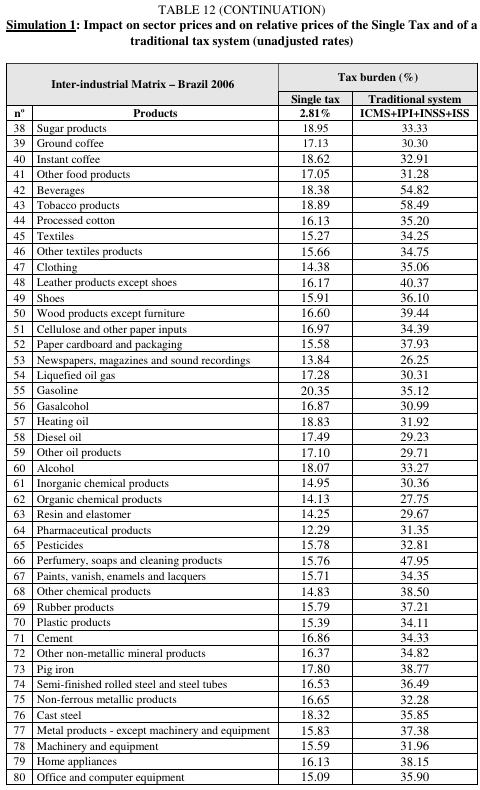
Simulation 1 in TABLE 12 compares the impact a bank transaction tax as a Single Tax would have on relative prices, compared to a conventional tax model. The simulation only includes indirect taxes, and does not include the foregone revenue raised by taxes on property (IPTU, IPVA, ITR, etc.), on personal and corporate income (IRPJ, IRPF), on foreign trade, and on other taxes that have extrafiscal or regulatory characteristics. Therefore, the simulation is strongly biased against cumulative taxes, because the tax rate applied to the bank transaction tax, of 2.81%, will raise more revenue (27% of GDP) than the conventional indirect taxes (ICMS, IPI, INSS, ISS) included in the simulation (10.9% of GDP).
One can see that relative price deviation for the bank transaction tax (Single Tax) was 2.38%, whereas, in the conventional model, it was 5.67%. This proves false the statement that cumulative taxes necessarily create greater distortions in relative prices. It should be noted that although in this particular case the result shows that a turnover tax was less distortionary than conventional taxes (mostly VATs), one cannot assert a priori that this always occurs, or that it never occurs. However, we can assert that under the circumstances of Brazil’s economy, this criticism to cumulative taxation did not prove true, as far as its effect on relative prices is concerned.
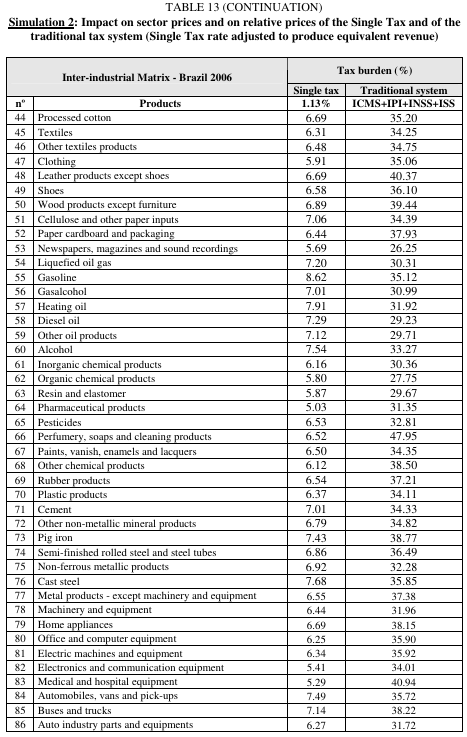
Simulation 2, in TABLE 13, introduces corrections to make the comparison more rigorous. The bank transaction tax rate was reduced to 1.13%, in order to force the revenue raised to be equal to that raised by the conventional taxes included in the simulation (10.9% of GDP). The conventional taxes, as in the previous simulation, are the ICMS, IPI, and ISS, and the employer contributions to social security (INSS). The effect of reducing the bank transaction tax rate from 2.81% to 1.13% caused the relative price deviations to drop from 2.38% to 1.13%, whereas the conventional model’s deviation remained at 5.67%. Deviations in relative prices caused by application of a cumulative tax were less than half the deviations observed in the conventional model, thus proving that the assertions to the contrary, made a priori, are erroneous.
Another interesting variation in the simulations addresses the oft-remembered alternative of eliminating the cumulative social contributions (the CPMF, a bank transactions tax, the Cofins, the PIS and the ISS, which are both corporate gross sales contributions), while maintaining intact all other components of the current Brazilian tax model, including tax revenue. The results can be seen in TABLE 14.
TABLE 12
TABLE 14
The explicit introduction of tax evasion into the simulation model, and its impact on distortions in relative prices, is another interesting topic for future research. The hypothesis assumed in this text is that tax evasion introduces strong elements of instability, volatility, and randomness in relative prices. Simulation 4, in TABLE 15, applies the same parameters as in Simulation 1, but introduces tax evasion into the model.
To this end, the same tax rates used in Simulation 1 were used again, but adjusted for estimates of the weight of the formal sector on the total Value of Production for each sector, as calculated by the BNDES. In other words, we estimate effective tax rates on the formal economy by adjusting the statutory rates to the proportion of informality in each respective sector.
For example, whereas in the sugar industry 100% of the sector is formal, in agriculture 93.1% is not a part of the formal economy. Applying corresponding information for the 110 products used in the simulations, we made equivalent adjustments to each sector’s tax rates, except for the rate of the bank transaction tax (Single Tax) because it is evasion-free even for those economic agents operating in the informal economy. The expectation is that the deviation of relative prices in the Single Tax model will remain constant, because the rate had not changed. But we expect, for the reasons mentioned above, that deviations in relative prices in the conventional model would be higher than the 5.67% found in Simulation 1.
The tax adjustment was done as follows. To the extent that we admit that evasion exists, stimulated by the high rates of conventional taxes, the drop in effective rates will imply a loss of revenue. To correct this, nominal rates of conventional taxes are raised by a proportion derived from the ratio of the sum of nominal rates to the sum of effective rates. The expectation is that in making this correction the higher nominal rates will offset the effects of evasion on tax revenue.
This is, in fact, what happens. The more tax evasion increases, the more the government increases nominal tax rates to offset the loss of revenue. This means that although rates and tax incidence patterns are altered, revenue is kept constant by raising statutory tax rates. In other words, this mechanism makes good taxpayers pay for bad ones.
After such adjustments were made, our hypothesis was confirmed by the simulation. Tax evasion had a strong distortionary effect on relative prices. The dispersion index jumped from 5.67% in simulation 1 (which assumed no tax evasion) to 7.72% in simulation 4, which incorporated tax evasion in the model.
These results strongly suggest the inadequacy of the peremptory and unconditional assertions, made by several scholars and critics of cumulativeness, concerning the distortionary effects of turnover taxes on relative prices, as compared to value-added taxes.
With these observations we hope to be marching ahead in understanding the last pending issue in the Single Tax controversy: that one cannot state a priori whether cumulative or value-added taxes introduce greater distortions in relative prices in the economy. But we can state unequivocally that in the empirical case of the Brazilian economy, bank transaction taxes such as the CPMF are less distortionary than the conventional tax structure made up mostly of value-added taxes.
3
TAXATION IN BRAZIL
INTRODUCTION
A first-time analyst of the literature on tax reform in Brazil would come to a curious conclusion: that the bulk of the controversy surrounding the subject, which dates back to the mid-1990s, focuses almost exclusively on doing away with cascading, or turnover taxes.
In fact, in August 2001, representatives of Brazil’s major business associations published a manifesto demanding an urgent tax reform.122 A close look at the document, however, shows that the true goal of business leaders was neither to discuss the tax issue as a whole – its malfunction and dysfunction – nor to seek comprehensive and definitive solutions to the problem. Rather, it was a severe criticism of cumulativeness present in some of the taxes in use in the country. Those entrepreneurial groups convinced important public opinion leaders that the top priority in tax reform should be nothing more that the elimination of turnover, cascading taxes.
One indicator of their mistake can be gauged in the results of a survey taken by
the National Confederation of Industry, in which 88% of business leaders surveyed pointed to Brazil’s excessive tax burden as the least desirable feature of the current tax system, and not to the presence of turnover taxes. Thus, it is surprising that business leaders have aimed their anger at cumulativeness, instead of arguing for a reduced tax burden and for lower tax rates.
The manifesto contained no demands for fighting tax evasion and corruption. Nor did it call for actions to decrease the high compliance costs related to accessory tax obligations imposed on taxpayers. It did not even complain about bureaucracy or about the inequities of Brazil’s current tax system. The manifesto complained almost exclusively of cumulativeness, despite the fact that what truly suffocates competitiveness in Brazil is not the manner in which taxes are collected (cumulatively or on value-added), but rather the disproportionate weight of Brazil’s tax burden, in excess of 34.8% of GDP in 2007. They were discussing form, and forgot the essence of their problem.
No heed was given to basic problems, such those raised by Everardo Maciel, former Secretary of Federal Revenue who foresaw that “without a doubt, the speed and depth of changes facing the world will affect (or even exhaust) the tax models in use today. Which taxes, then, will continue to exist, or which new ones will be created, are still questions that have no answer.”
Tax evasion, not the CPMF, is the tumor that must be rooted out from the national tax system, and no other system, apart from the bank transaction tax, can do just that. As a matter of fact, the CPMF and bank transaction taxes are not problems in Brazil’s tax system; rather, as assumed by the Federal Revenue Service,” Brazil can prove that the use of bank transaction taxes…can be the solution for taxation in an increasingly globalized and electronically dependent world”.
This text discusses Brazil’s tax system, including its cumulativeness. We demonstrate that a priori rejection of cumulative taxes is the result of prejudice and of poorly digested theoretical concepts. We will also show that it is important to overcome this erroneous and incomplete interpretation of Brazilian tax problems. This is the first step to begin building a more efficient tax model, capable of being more equitable, less costly, and more consentaneous with Brazilian economic and social structures. Such tax model, as will be demonstrated, is the Single Tax system.
BRAZIL NEEDS A NEW TAX SYSTEM
Brazilian society shows signs of deep dissatisfaction with its tax system . It is one of the most complexes in the world, having reached an advanced stage of deterioration, irrationality, inefficiency, and inequity.
In mid-2001, Brazil’s tax legislation consisted of 55,767 articles, 33,374 paragraphs, 23,497 sub-paragraphs, and 9,956 headings. This tax law miscellany is housed in 18,589 pages of texts, decrees, codes, and notices. These figures, however, need to be updated each day. Every year nearly 300 new laws are drafted on the subject – roughly 1.23 alterations per business day.
In less than three years, between May 1995 and December 1998, legislation related to two federal taxes (the Income Tax (IR) and the Industrialized Products Tax (IPI)), one state tax (Circulation Tax on Goods and Services (ICMS)), and two Social Contributions (Social Integration Program (PIS) and Social Security Contribution (Cofins)) increased in the following manner:
• On the IR: 24 laws, 76 provisional measures, 14 decrees, 46 notices, and 149 rulings;
• On the IPI: 8 laws, 41 provisional measures, 20 decrees, 67 notices, and 87 rulings;
• On the ICMS: 24 laws, 165 notices, 314 resolutions and conventions;
• On the PIS: 1 Constitutional Amendment, 7 laws, 122 provisional measures, 1 decree, 3 resolutions, 8 rulings, 3 notices, 1 court order, and 1 legal opinion;
• On the Cofins: 2 supplemental laws, 3 laws, 30 provisional measures, 1 decree, 1 notice, 1 court order, and 1 ruling.
A recent study done by the Instituto Brasileiro de Planejamento Tributário (Brazilian Institute for Tax Planning) estimated that between October 1988, when the new Brazilian Constitution was promulgated, and October 2008, over 240,000 pieces of tax regulation and legislative acts were issued, which amounts to 34 pieces of legislation issued each day since 1988, including week ends and holidays.
Such complexity, typical of declaratory taxes is not unique to Brazil. In the United States heated debate has been waging over changes in that country’s main source of revenue, the income tax. Current US federal tax law is contained in no less than 45,662 pages, a number which has grown by 74% since 1984. Between 1990 and 2000, the number of tax forms increased by 23%%. The eight largest taxconsulting firms experienced sales increases of 112% between 1996 and 2001. The American “tax industry” currently employs over 1 million people, more than the entire automotive industry. US taxpayers spend US$ 183 billion annually in compliance costs alone (filling out forms and returns).
In Brazil, the excessive number of taxes has directly contributed to record increases in revenue, year after year. TABLE 16 shows the growth of the tax burden in Brazil.
Some argue that the tax burden, as a percentage of Brazil’s GDP, could increase, considering that in several developed countries they are still higher. However, such an opinion is nonsensical if taken as an isolated statement. A country’s tax burden can only be appraised considering, comparatively, its per capita income levels and its stage of development.
TABLE 16
TABLE 17 shows the tax burden in selected countries. Brazil carries a tax burden that is incompatible with the per capita income level of the population. All countries bearing a tax burden near or higher than 30% of GDP have per capita annual income of US$ 40,000 or more. It is worth noting that countries with per capita income of less than US$ 10,000 per year have tax burdens of less than 25% of GDP. Brazil (and Uruguay in this sample of countries) is a clear example of extravagant over taxation.
Brazilian consumers bear high indirect taxes built into prices of products and services. According to ABIA [Brazilian Food Industry Association], taxes account for up to 34.7% of the final price of food. Internationally, the average is 7%. TABLE 18 illustrates the abusive taxation of consumer goods in Brazil, which results in low purchasing power of wages and in loss of competitiveness of Brazilian products in foreign markets. Most taxes on domestic production are not exonerated at the time of export, making exported goods and services carry heavy tax loads built into their prices (tax export).
In order to defend themselves from such an abusive tax burden, taxpayers practice evasion as a dodge necessary for survival. Tax avoidance has become a behavioral rule for Brazilian taxpayers, to the point of being called a “national religion”.
TABLE 17
In 1999, the Secretary of the Federal Revenue, Everardo Maciel, testified before the CPI [Parliamentary Investigative Commission] on the Financial System. His statement caused a strong impact on public opinion. The country was officially informed that large-scale tax evasion, tax avoidance, and other forms of tax hiding were common practices. According to his testimony, R$ 825 billion, almost one year of Brazil’s GDP, slipped through the fingers of the Federal Revenue without a cent of it being collected, except for a small amount of revenue collected by the CPMF (a turnover bank transactions contribution). He stated, furthermore, that half of Brazil’s 530 largest corporations had not been paying income tax, and 42% of the 66 largest banks had accomplished the same feat.
Tax evasion is a deadly tumor to be extirpated from the nation’s tax system. The prevalence of this anomaly is responsible for deep tax injustices. According to the proceedings of the CPI [Parliamentary Investigative Commission] on Tax Evasion, “tax evasion is entrenched in the population, in taxpayers, due to an educational and moral problem.”
The Federal Revenue has been cross-referencing bank transaction data with filed income tax returns. The data reveal that billions of reais circulate free from the reach of the income tax.
TABLE 18
In 1999, cross-referenced data uncovered taxpayers who claimed to be exempt
or economically inactive, and firms registered under the Simple [simplified tax procedures for micro and small firms], but whose bank transactions, surprisingly, amounted to approximately half of Brazil’s GDP, as shown in TABLE 19. It is worth noting that 559,161 individuals and firms transacted a total amount of R$ 116.9 billion, a monthly average of R$ 9.74 billion, while “claiming” to be exempt from income tax (of those, 424,435 individuals and firms that transacted R$ 77,736 billion were suspected of evasion, as seen in TABLE 19).
The data also revealed that 254 individuals and firms transacted the overwhelming amount of R$ 164.1 billion without paying income tax. On average, each one transacted R$ 54 million per month, but claimed to be exempt, inactive, registered under the Simple [simplified method of tax calculation used for small and micro firms], or were outright omissive. The analysis concluded that in 1999, 512,117 individuals and companies transacted R$ 465.5 billion, or R$ 38.8 billion per month, without reporting such payments to tax authorities. Implicitly, such transactions represented evaded earnings estimated at R$ 339.2 billion, or R$ 28.3 billion per month. In other words, transactions equivalent to approximately 32% of GDP evaded Brazil’s income tax.
Tax avoidance makes the current pattern of tax incidence on production so chaotic, unpredictable, and devastating that it can bankrupt an efficient taxpaying company. On the other hand, it can enable an inefficient tax-evading producer to survive, by looting its competitors in the marketplace.
TABLE 19
According to surveys, 40% of Brazil’s income are not reported to tax authorities due to evasion or to escaping into the underground economy. This figure implies that the current tax burden of 38% of GDP is borne by 60% of potential taxpayers; in other words, those that pay bear a tax burden of almost 65% of their taxable income, while evaders contribute little to society, or much less than they should.
Furthermore, tax evasion has an inevitable consequence: corruption. In Brazil, tax avoidance and evasion are accepted as normal facts of life, and are often praised as signs of courage and boldness in market behavior. Collusion between tax evaders and corrupt tax officials has been a cause of severe deterioration of ethical and moral standards of Brazilian society.
But it is on labor income that Brazilian tax burden sets a dreary record.
The combination of widespread tax evasion and the need for increased public revenue has turned payroll employees into one of the most heavily burdened subjects of taxation. Because of greater difficulties in practicing evasion or avoidance, regularly hired payroll employees are easy prey to escalating taxation. Additionally, the government has overburdened employers with extremely high fiscal and social security obligations.
Labor income in Brazil, which accounts for only 26.8% of domestic income, bears the burden – directly and indirectly – of approximately 53.5% of the country’s tax revenue. This provides clear indication that, in order to compensate for revenue lost to evasion, the government transfers the tax burden to those for whom tax evasion is all but impossible, namely, payroll employees. Data from both the US Internal Revenue Service and the Federal Revenue show that in the United States the individual income tax rate increases from 15% to 19% as taxable wage income reaches R$ 119,200 annually. In Brazil, the same rate increase is triggered when taxable income reaches R$ 15,200 per year.
This fact contributes significantly to current high unemployment rates. Furthermore, the high cost of hiring and maintaining payroll employees is one of the key causes of the growth of the informal economy. Half of Brazil’s workers are not formal payroll employees.
Another characteristic of the Brazilian tax system is its regressiveness. In fact, ex post the system taxes more heavily those with lower income, although statutory taxes are usually progressive in their formal mechanisms of tax collection. For example, the income tax is progressive ex ante, but becomes regressive ex post after evasion and all deductions and allowances are duly accounted for. On the whole, the Brazilian tax system is regressive, as found in a recent study that showed that the tax burden for families earning up to two monthly minimum salaries is 48.8%, while it falls consistently across higher income brackets until it reaches a tax burden of
26.3% for families earning more than thirty monthly minimum salaries.
These facts demonstrate the urgent need for tax reform in Brazil. This is a debt contracted by government and by politicians with regard to Brazilian society during the last decade of the 20th century, and still left unpaid. Despite various attempts, tax reform never happened. The debate was intense; at times, even passionate. But it was never carried out.
It is no simple task to accommodate the specific interests of the vast number of social groups involved in a tax reform. These groups include workers, business men, and government agents, which are further divided by sectors and geographical areas, often with conflicting interests. Each group envisions in tax reform an opportunity to broaden its own economic space. Such conflicting interests cannot be resolved by conventional tax reform, as past experience has shown.
The Single Tax proposal for a tax reform, as will be shown ahead, by allowing gains to all parties involved – the public sector, payroll employees, and business owners – creates favorable conditions for a productive discussion. For the public sector, the Single Tax allows for reduced costs, for dismantling of unnecessary bureaucracy, for administrative modernization, for recovering evaded revenue, and for a lower public deficit; for workers, it allows for wage increases through the transfer to personal earnings of part of the social security contributions and payroll withholdings. For business owners, it allows for reduced costs, for larger markets, and for higher profits and investments.
Antonio Ermírio de Moraes, head of the largest industrial group in Brazil, stated in a published interview that he had engaged his entire legal and tax departments to analyze the Single Tax and the bank transaction tax, concluding that it is evasionproof. With a Single Tax, only tax evaders and the underground economy stand to lose, but this would be a welcome act of Justice, long overdue.
ROBERTO CAMPOS: THE CHOICE BETWEEN “INNOVATIVE INSOLENCE” AND “PERFECTING THE OBSOLETE”
Roberto Campos was an enthusiastic supporter of new ideas, of innovative insolence, and of the Single Tax. Such posture surprised those who claimed that “Bob Fields” was a starch conservative (“Bob Fields” is the literal translation of his name, as he was jokingly known because of his support for economic liberalism, and for his fierce defense of free market ideals). They were wrong. He was always original, an iconoclast, a creator of new paradigms.
Between 1964 and 1967 he was responsible for implementing the last tax reform in Brazil. He introduced changes that cleared the way for what was called the “Brazilian miracle” of the 1970s, a period of outstandingly high economic growth.
During the 1980s he became a respected politician and a critic of the government. He claimed that the state apparatus had become deformed, grossly deviating from its original objectives. He pointed to several problems that required urgent solution if the country were to build a modern and prosperous economy. On one occasion he said, “We remain too far removed from achievable wealth, and too close to correctable poverty.”
During the last ten years of his life, one of his major criticisms was directed at taxation in Brazil.
He showed that value-added taxes, VATs, which are widely acclaimed as fair and efficient, actually hid another far less attractive reality. The deformities hidden in that invisible reality are amplified in countries with federative systems of government: bureaucratic exacerbation, rampant corruption, exasperating complexity, prohibitive operational costs, irresistible tax avoidance, and everseductive evasion. He claimed that a VAT tax is a monster of the declaratory genus, of the bureaucracy-bribery species, beloved only by busybody private and governmental bureaucrats.
In “Reform or Revolution” Roberto Campos stated that Brazil’s fiscal ethics had been destroyed. He insisted that to pay taxes was to purchase harassment and irritation, and that only firms in the formal economy and registered payroll employees actually pay direct taxes. The remaining taxpayers, estimated by him to account for two thirds of the total, were tax evaders, which he referred to as delinquents.
In tax matters, between reformist simplifications and revolutionary innovations Roberto Campos preferred the latter. He supported the proposal of a Single Tax, which he considered a seminal idea. He wrote that “On fiscal matters the country has the chance to introduce a pioneering experience with the Single Tax. This is so because of the coincidence of circumstances inexistent elsewhere: a) both fiscal ethics and the tax structure have begun to collapse; b) the economy became nonmonetized (free of paper currency) – paper currency in the hands of the public amounts to less than 1% of GDP; c) the banking system is surprisingly modern and electronically equipped for a third world country.” Campos concluded by stating:
“As I see it, the (desired) features of a fiscal revolution would be: 1) a tax base sufficiently broad and simple to turn innocuous the frontiers between taxpayers and criminals; 2) rates sufficiently low to make unprofitable tax-engineering attempts at finding evasion schemes; 3) automated tax collection that would make dispensable the three levels of federal revenue bureaucracies (municipal, state and federal); and 4) instantaneous transfer of tax proceeds to their beneficiaries, avoiding the complications of tax indexing. All of these conditions are met by Professor Marcos
Cintra’s proposal (the Single Tax), and by none of the reformist proposals.” Roberto Campos became a Single Tax warrior. He emphasized the need to implement this system exactly as it had been idealized; in other words, as a tax that would replace all fiscal taxes (those primarily purposed to raise revenue). Meanwhile, in 1992, the government, seized by a tax collecting fury, made an opportunistic use of the basic pillar of the Single Tax, the bank transaction tax, and created the IPMF (Provisional Bank Transaction Tax), which later became the CPMF (Provisional Bank Transaction Contribution). But they were used as additional taxes, in a regrettable violation of the original intent to have a single hegemonic tax.
The creation of the IPMF/CPMF provided Single Tax critics with a valuable opportunity to demonize the bank transaction tax. A myth was painstakingly constructed, which stated that, because of its cumulativeness, the tax was necessarily inefficient, of low quality, and therefore should be fiercely rejected.
Tax evasion – the foremost anomaly of the Brazilian tax system and which the Single Tax proposal emphatically addressed – was relegated to a secondary level of interest in the subsequent debates on tax reform, thus allowing the sprouting of a perverse competitive advantage: continuing and unabated tax evasion allows inefficient firms to survive, as long as they continue practicing it, while more efficient, but evasion-shy firms, succumb to tax fraud and to unfair competition.
Sarcastically, Roberto Campos made a distinction between two kinds of cascade in taxation: one, malign and the other, benign. Malign cascading taxes are those such as PIS and Cofins (taxes on gross income of firms), which are notoriously less prone to evasion. Benign cascading taxes, on the other hand, are those that reduce fiscal obligations to taxpayers, such as the Simple (simplified tax system also called the Single Tax for micro and small businesses), or the corporate income tax option for assessment based on “presumed profits”, a fixed proportion of gross income of firms.
Not surprisingly, criticism is always directed at the first group of taxes. Whenever the cascade involves obstacles and restrictions on evasion, and therefore a higher tax burden, it is swiftly seen as diabolical, and therefore as malignant. But whenever a tax model, even if grossly cumulative, reduces the tax bill, the cascade is considered benign, even by hard line critics of cumulativeness. Such bias can be clearly seen in the crusade against the CPMF, the only tax in Brazil that has been proven impossible to evade.
Roberto Campos argued in favor of “reformatting the State”, and gave special emphasis to the Single Tax proposal. Throughout his brilliant career, his privileged mind was always capable of seeing far beyond. He demonstrated clearly and unequivocally that tax reform is a fundamental demand for approximating “achievable wealth” and for combating “correctable poverty”. But unfortunately, discussions about tax reform in 1999 resulted in a report issued by the Special Commission on Tax Reform of the lower house of Brazilian Parliament that Roberto Campos qualified as a futile attempt “to perfect the obsolete”.
Among his many memorable articles there are some that deserve extensive reproduction.
In “The Funeral of the Invoice” and in “How to Get Out of the Madhouse” Campos describes, in his usual masterful style, the dichotomy of current tax debate, as reflected in the bloody duels between those who support conventional tax models and those who seek new bases on which to build a modern tax system.
In the first article, Robert Campos says, “two concerns afflict analysts of
‘Brazil’s sovereign risk’ in both the medium and long terms. The first is our “fiscal madhouse” (costly tax collection and multiple forms of evasion), which creates a sinister dilemma: whether to increase tax rates, thereby weakening taxpayers, or to sacrifice essential investments. Fiscal disorder is acutely seen in the Executive branch, moderately in the Legislative, lightly in the state and municipal governments, whereas the Judiciary continues to be fertile at granting injunctions to protect ‘acquired rights, or abuses’. The second concern is the insolvency of the ‘pay-as-you-go’ social security system, which is structurally deficit-ridden.…In fiscal matters, we are achieving a primary budget surplus thanks to emergency (once and for all) revenue that only further complicates the tax structure. Any effective reform must take into consideration three facts: 1) hired labor is taxed excessively, leading to informal jobs or unemployment. Furthermore, taxes and union dues are shrinking worker’s ‘take-home pay’ (net wages); 2) declaratory taxes that require abundant paper work – IR [Income Tax], ICMS [Circulating Sales Tax on Goods and Services], IPI [Industrial Sales Tax], ISS [Tax on Services], etc. – and involve three levels of bureaucracy: tax compliance, auditing by the Federal Revenue, and often the litigation process; 3) Brazilian cultural tradition is prone to fiscal rebellion, due to the anemic supply of government services, the system’s complexity, and corruption among tax officials. This makes unproductive those taxes that rely on declaratory paper returns from taxpayers.
“Taxes must be automatic, collected electronically at the root of the economic process. There are bills in Congress, such as those sponsored by Congressmen Marcos Cintra and Luís Roberto Ponte, in which the bank transaction tax, and special excises (called selective taxes) on essential inputs – electricity, fuel, vehicles, and telecommunications (in addition to cigarettes and alcoholic beverages) – would replace all other declaratory taxes based on paper tax returns. Collection would be done electronically, dramatically reducing costs and the gymnastics of tax avoidance.
“The Government’s proposal to replace current taxes with a federal VAT has obvious merits, such as simplification, but it merely improves the obsolete, since taxes would continue to be paper-driven and to be assessed by a highly bureaucratic procedure.
“Classical tax structure, to which we hold so firmly, is a curious handicraft relic in the electronic age. An alternative is the bank transaction tax embedded in a Single Tax model, which nevertheless, faces some spurious objections. One of the objections is its alleged ‘cascade’ effect, which in reality is a benign form of ‘progressiveness’, because it affects more than proportionally the rich, who make comparatively more bank transactions and purchase more products with long productive chains. The other objection has to do with the tax federalism and the autonomy of states and municipalities. But this autonomy is more adequately preserved when state and local government are granted guarantees of automated collection of revenue and availability of funds for spending, than the illusory power to create evasion-ridden taxes that require costly fiscal bureaucracy to raise revenue. States and municipalities would be given their revenue shares without any bureaucratic or political intermediation.
“Partisans of electronic taxation now have a powerful ally in the search for new fiscal technology: internet e-commerce, which is growing at an annual rate of 70% in the United States. This explosive growth, which weakens the effectiveness of the sales taxes, will have as an inevitable consequence at least: 1) a unification of state and local tax rates and classifications; and 2) a mechanism to centralize tax collection. Last February, the United States Governors Association issued a manifesto that favors the creation of a ‘21st Century sales tax applicable to the Net’. Everything points to the Internet as the funeral for tax invoices, in the same way the fax was the tomb of the telex and airplane, the exterminator of air-balloons.”
In the second article, Roberto Campos says that “for some time now I have considered the deconstruction of our fiscal madhouse to be extremely urgent, in order to correct two major evils: tax evasion, which divides the country into ‘taxpayers’ and ‘free riders’, and the high cost of labor, which causes informal work relations or unemployment.”
“Today, there is a third reason, because globalization and digitalization represent a ‘paradigm shift’. The productivity of classical taxes on production, circulation, and services has been greatly diminished; these are homespun relics in the electronic society. There are many reform proposals, all affiliated with one of two lines of thought: that of the ‘papyrophiles” who limit themselves to simplifying the paper and document-driven system, and that of the ‘eletronicphiles’ who wish to abolish classical paper-driven declaratory taxes that presuppose that taxpayers will correctly and dutifully fill out tax returns for income, sales, and services…(which) on one hand increases compliance costs, and on the other, facilitates tax evasion.
“The major proposal now in Congress is the preliminary report written by Congressman Mussa Demes, of the Special Commission on Tax Reform. It is an effort to ‘perfect the obsolete’, because it would replace the ICMS, the IPI, and the ISS with a new ICMS (a value-added tax) under federal legislation and shared with the states. Being a tax under responsibility of both federal and state governments, it would have double auditing and collecting operational jurisdiction. Furthermore, if the new ICMS were to incorporate the social contributions – PIS, Cofins, and CSLL [Social Contribution on Profits] – the current 17% rate would have to be increased in order to substitute for their lost revenues, further stimulating evasion.
“The other approach to tax reform adopted by the ‘electronicphiles’, was the object of a bill presented by Congressman Luís Roberto Ponte, already approved by the Special Commission on Tax Reform . However, it was never brought up for a vote on the floor of the House due to the opposition from the Government, which prefers topical micro-adjustments in the tax system to radical changes. Fortunately, Congressman Marcos Cintra has just introduced in the lower chamber an ‘alternative proposal’ which smoothes out the original idea of a ‘Single Tax’ on bank transactions, and attempts to reconcile the two opposing lines of fiscal thought.
“There would be few taxes; almost all non-declaratory. Current property taxes (IPVA [Motor Vehicle Tax], IPTU [Urban Land and Property Tax], and ITR [Rural Land Tax]) would be preserved, as would regulatory taxes on foreign trade and on credit (IOF [Tax on Financial Transactions]). Due to the insistence of state capital cities, which extract approximately 25% of their revenue from the service tax (ISS), it would remain in force, as opposed to the Demes proposal of a new retail sales tax for municipalities, which is costly to collect and easy to evade.. One significant advance is to replace the panoply of social contributions – Cofins, PIS/Pasep, CSLL, and the employers’ payroll contribution – with a global tax on bank transactions, purged of the imperfections of the CPMF. The income tax, which at its heart is a socialist rascality because it punishes those who are most diligent and creative, would be compacted. Individuals earning up to 20 monthly minimum salaries would be exempt. The corporate income tax would be abolished.
“It is a tenacious illusion to think that firms are the ultimate taxpayers. Taxes always fall upon individuals, whether stockholders, through losses in earnings, workers, through paycheck withholdings, or consumers, through higher prices of goods. To stimulate reinvestment, in the Cintra bill, profits would only be taxed if distributed to individuals.
“Abolition of the employer’s contribution to the INSS [National Social Security Tax] would encourage employability in the formal sector. If we want deep and lasting fiscal reform, we must take into consideration the effects of globalization and digitalization. Today, a transnational corporation can choose to account its profits or purchase its components in whatever country has the most benign and least bureaucratic fiscal system. Then again, how should labor regulations treat a “telecommuter” who works for companies located in another country?
“The fairest tax is not the one that best redistributes income (because social justice is best handled on the spending side of the budget), but rather the one that is most evasion-proof and inexpensive to collect.
“The bank transaction tax, replacing the CPMF, would be the most appropriate system in a digital economy such as Brazil, but unfortunately it has been demoralized by its ‘cascade effect’. Nevertheless, it should be seen as one of those benign cascades since revenue collection is free of bureaucracy and almost evasionproof, as opposed to the malignant cascades implicit in the Cofins and PIS/Pasep (declaratory gross revenue taxes totally dependent on reported sales). The bank transaction tax will seem much friendlier if acknowledged as a ‘progressive tax’, since it is levied mostly on the wealthy, who conduct larger transactions and purchase sophisticated products that have extensive production processes. Only two of the objections to the cascade are relevant.
“The first is the negative effect on high-speed transactions in the stock market. This has led Congressman Marcos Cintra to propose that taxation only be applied to realized earnings, and not to transactions within the capital markets.
“The other has to do with the alleged impossibility of allowing tax credits on exports. The solution lies not in tax credits but on ‘rebate’ procedures allowed by the WTO. That is, restitution to exporters of amounts equivalent to the average tax burden extracted from embarked products, calculated according to Leontief’s inputproduct tables which are now routinely available from the IBGE (Brazilian Institute of Geography and Statistics). This is preferable to the current and highly conflicting procedure of compensating the exporting States for the hypothetical loss of revenue due to exemption of ICMS in foreign trade. Replacing the ICMS with an excise tax on electricity, fuel, telecommunications, vehicles, alcoholic beverages and tobacco, collected electronically as they leave their production loci usually concentrated in a few large plants, would have several advantages: no evasion, less bureaucracy, automatic partition and delivery of revenue, electronic tax collection, and full compatibility with the digital age.”
Roberto Campos concludes by saying, “It surprises me that Congressman
Cintra’s ‘alternative proposal’, which is more modernizing and simplifying than the Government proposals found in the Demes report, has been discussed so little in Congress and by the press. It would be melancholic if, in the electronic age, we were to remain subject to the papyrophilia of classical taxes’.”
In the article “The Fiscal Madhouse”, Roberto Campos illustrates with great precision the tax atmosphere in Brazil during the 1990s. He says that “one of the myths that have hindered tax reform has been the belief that an essential requirement of federative autonomy is to preserve the three separate tax revenue machines at the three levels of government. Some federations, such as Germany, have centralized tax collection. The true autonomy and independence of states and municipalities rest in their freedom to spend according to their own priorities. The method of tax collection should be the simplest and cheapest possible, and funds should be partitioned and delivered automatically and instantaneously.
“Among conventional declaratory taxes – income, consumption, and services taxes – the progressive income tax, considered to be the most equitable by neoconservative leftists, is precisely the most inadvisable in developing countries. There are three possible principles of equity: a) the benefit principle, taxing individuals according to the benefits they draw from public services; b) the liberal principle, according to which individuals should be taxed proportionally to their consumption, that is, to the use they make of society’s production; c) the socialist principle, according to which individuals should be taxed progressively, according to their ability to pay, which reflects the contribution they make to society through their productive efforts.
“The socialist principle is anti-development. It creates disincentive to savings and investment – precisely the opposite of what is advisable for a developing country. In the extreme case, defended by foolish leftists, in addition to the tax on current income, accumulated income should be taxed again (wealth tax on large fortunes), with the resulting effect that capital accumulation would take place elsewhere, and not within our Tropic of Capricorn.
The insufficiency of internal savings is driving even industrialized and rich countries such as the United States to consider replacing progressive income taxes with a Flat Tax, that is, a single rate applicable both to businesses and individuals, levied only on consumed income and not on produced income (of course, with generous exemption for the poor).”
Roberto Campos continues, in “Jatene’s Revenge”146 : “my position on the subject has always been clear. I consider, in theory, that the Bank Transaction Tax is the most modern and efficient tax collection instrument. Its use only became viable on a large scale with the advent of electronic banking payment systems. Essentially, it is a creature of the electronic age. Instead of taxing subsets – such as income, services, and merchandise circulation – we would tax a synthesis of them all – the bank transaction – which in modern economies is a faithful reflection of all economic transactions and payments. I opposed the IPMF (a temporary bank debit tax introduced in 1992-3) because it was just one more tax, in addition to the existing ones. It simplified nothing. It adopted the ‘methodology’ of a single tax, eliminating fiscal bureaucracy, but it violated the philosophy of the single tax, which is the ultimate simplification of the system as a whole. In 1996, I accepted the CPMF (the former bank debit tax was turned into a contribution), albeit with discomfort, surrendering to Jatene’s argument [Dr. Adib Jatene, former Health Minister] that the public health network was facing imminent collapse, with no available fiscal alternatives. Spending cuts and reformulation of the corrupt health system would only produce results over the medium and long term.
“I do not have the least respect for the conventional wisdom that enthrones classical taxes as indispensable, such as income tax and value-added taxes on sales of goods and services. Both are intolerably obsolete. They lead to the creation of parasites, social classes such as tax officials and tax professionals, who do not profit from productive activities, but rather from ‘exploiting complexity’. All declaratory taxes, which require paper returns (income, consumption, or services taxes), involve two bureaucracies: the taxpayers’ and the auditors’. The more complicated the tax is, the greater the profits of the parasites. In Brazil we achieve the maximum waste with five tax collecting machines: municipal, state, federal, labor, and social security.
“A good tax is neither an ‘old tax’ nor a ‘classical tax’. A good tax is one that is evasion-proof and is automatically collected. Any tax that can be evaded is socially unfair. And if collection depends on tax reporting paperwork, it becomes a waste. The features of a tax that is automatic and evasion-proof are precisely the features of the Single Tax on bank transactions, which have not found support from the Government or even from Congress.
Roberto Campos concludes: “unfortunately, the simplifying methodology of the bank transaction tax has been demoralized by the fact that the Government has twice – with the IPMF (1993) and with the CPMF (1996) – used the tax’s automatic ‘methodology’ without paying heed to its simplifying ‘ideology’. An otherwise sophisticated instrument has been ruined through misuse, like a fencing foil being used for cutting sugar cane…”
The most curious element of this debate, the flavor of which Roberto Campos captured so charmingly in his newspaper articles, is that representatives of the entrepreneurial classes do not understand their own reality and do not tend to their own interests when they oppose the bank transaction tax solely on the basis of its cumulativeness. Over 90% of Brazilian firms voluntarily subject to cumulative taxes through tax methods and systems that are widely accepted and openly praised by the business community, although only applicable to micro and small firms. These methods are widely adopted not by imposition of tax agencies, but by free choice of those same people who, exhibiting a contradictory stand, advocate the immediate elimination of turnover cascading taxes in exchange for declaratory value-added taxes (VATs).
THE CONTROVERSY BETWEEN THE CENTRAL BANK AND THE FEDERAL REVENUE ON THE CPMF
The Brazilian Central Bank issued two reports analyzing the economic impact of the CPMF. It took a clear position against levying the CPMF on transactions performed in the financial and capital markets.
It should be remembered that just before the announcement of the timid tax reform of 2001 the president of the Central Bank, Armínio Fraga, stated that the government had at last decided to exempt such transactions from the incidence of the CPMF. The exemption was not immediately granted, as the Central Bank had expected, and this may have motivated publication of the two papers as a means of putting pressure on economic authorities to allow the planned exemption, which was finally enacted only in 2004.
In general, the allegations of the Central Bank pointed in two directions. First, the drop in transactions performed in the Brazilian stock market was attributed to the effects of the CPMF. Secondly, it was stressed that the turnover tax was having strong effects on interest rates, thus explaining their high levels.
Actually, since the very beginning of the debate over the Single Tax on Bank Transactions, attention had been drawn to the inadequacy of applying such tax on the financial and capital markets. A financial investment is strictly an operation that involves renting money, or capital. Thus for the same reason that the CPMF is not imposed on the value of real property each time a lease contract is renewed (it is imposed only on the flow of rents, and not on the stock of real estate capital), it must also not be levied on the value of the principal in a financial transaction each time a contract is due, or an investment is reissued, or rolled over.
When the Government introduced the Provisional Tax on Bank Transactions (IPMF) in 1993-1994, which was followed by the CPMF in 1997, it did not exempt transactions in the financial and capital markets, although it was full aware that the cumulativeness of the IPMF/CPMF impacted these markets, especially the structure of interest rates.
Albuquerque, the author of one of the Central Bank’s papers, lists various reasons for criticizing the bank debit tax. He addresses the CPMF as a bad tax, which shows “significant deficiencies as a revenue instrument”, among them its impact on interest rates “in a manner disproportional to other taxes” and which, as a consequence, increased government expenditures in servicing the public debt. In addition, he mentions other criticisms to the bank transaction tax, like the disincentive to using banking services, the illiquidity in the financial markets, which diminishes the incentives for increased use of credit, and its high dead-weight losses.
Notwithstanding the imprecision of some of these claims, the paper presents an incomplete and biased analysis of the problem, in addition to having methodological weaknesses, as pointed out in a paper by the Federal Revenue.
According to it, the validity of the conclusions of the Central Bank’s paper depends on some unlikely and unrealistic assumptions, such as the existence of perfect competition and of a completely specified production function. Furthermore, there are flaws in the specifications of the econometric model (such as not including relevant variables) and the possibility of a strong correlation in the residues of the selected variables, which might indicate a problem of spurious relations.
Technicalities aside, the Central Bank paper attempts to demonstrate that imposing the CPMF on financial markets leads to serious problems, whereas the Federal Revenue’s rebuttal has largely minimized the impact of such alleged effects. Arguments such as the inducement to excessive verticalization in the production process,152 the risk of bank disintermediation, and the lack of progressiveness and selectiveness of the CPMF, are issues which have already been thoroughly discussed during the 1990s, and which could be safely discarded as being devoid of practical interest. None of these risks has been empirically observed during the life of the CPMF.
Therefore, we shall concentrate on evaluating the validity of two more relevant criticisms, which are: the impact of the CPMF on interest rates, and the possible erosion of its base of incidence as nominal rate increases.
The claim that the CPMF has caused a significant increase in real interest rates can be rebutted quite easily, even though, coeteris paribus the CPMF does effectively lead to a higher cost of money. In other words, the criticism may be qualitatively true, but a quantitative evaluation demonstrates that this is a problem of minor importance.
The Central Bank model presupposes, without plausible justification, a totally inelastic demand for credit, which obviously magnifies the CPMF’s impact on interest rates. Based on that, the Central Bank paper asserts that the CPMF “contributes to the increase in the public deficit”. In other words, what it implies is that revenue from the CPMF is less than the increase in the public debt service that it may have caused. With CPMF revenue estimated at approximately R$ 19 billion in 2001, and accepting the exaggerated assumption that 40% of net public debt (approximately R$ 240 billion) is indexed to the Selic rate (rate of interest paid on government bills), the paper leads to the conclusion that the CPMF must have caused an increase of at least eight percentage points in nominal interest rates.
This is a gross exaggeration, as the Central Bank itself claims that the CPMF has had a 2.7% impact on Selic rates, 3.3% on consumer credit, and 5.9% on the interest rate charged on overdrawn bank account balances. Actually, the greatest impact on interest rates in Brazil does not stem from the CPMF, but rather from the banking spreads.
Several of the Central Bank’s papers claim that the influence of taxes on banking spreads is very modest, and that more important than taxes are the rates of interest demanded by savers, the operational costs of banks, and their profit margins. Even if we grant that interest rates demanded by savers are influenced by the CPMF, it cannot be denied that high interest rates in Brazil are more likely explained by the microeconomics of the Brazilian banking system, with its notorious concentration, its cartel-style organized trade associations, its high operational costs, and its high profit rates.
According to the Federal Revenue paper, to claim that the CPMF is responsible for Brazil’s high interest rates “is to jump to conclusions. The CPMF impacts interest rates in the same way as other taxes long imposed on bank transactions (such as the IOF, a tax on credit), countless fees charged on transactions and many other cost and profit items related to financial intermediation activities. Before reaching a conclusion... one must determine the true components of the banking spread (30.4 percentage points in January 2009), of which more than half is accounted for as banks’ gross profits, net of indirect taxes). However, it is well known that these factors are not the most relevant in determining Brazil’s interest rates. Interest rates represent, in synthesis, the market’s overall assessment of Brazil’s creditworthiness...” Thus, it can be seen that blaming the CPMF for the high costs of capital in Brazil is more likely a good excuse for justifying the banking sector’s high profitability.
Furthermore, an impartial analysis of an eventual increase in interest rates caused by the CPMF should consider the countervailing effect the CPMF may have had in reducing banking costs by replacing traditional paper-driven declaratory taxes, which are known to have much higher compliance and administrative costs.
In spite of the fact that the author of the Central Bank paper has not based his conclusions on reliable empirical data, and that he may be reaching conclusions that are highly speculative in their quantitative results, the fact is that a bank transaction tax does indeed tend to raise interest rates. And though this effect may not be very significant, and therefore should not be held responsible for the budgetary problems faced by Brazil’s public sector, the CPMF should not be imposed on the financial and capital markets, as I have been insistently pointing out since the earliest discussions about the Single Tax proposal, in the beginning of the 1990s.
This recommendation is not based on the CPMF’s quantitative impact on interest rates, but rather on a conceptual necessity. In this regard, the Central Bank paper’s arguments are well-founded, although for the wrong reasons. Nevertheless, it lays solid ground for not imposing the CPMF on the financial and capital markets.
It must be noticed, however, that the Single Tax proposal, which provides for the non-incidence of the CPMF on financial and capital markets, does not create any privilege whatsoever for them. Such transactions are taxed, albeit with a special procedure. In other words, we advocate the non-incidence of the turnover tax on such transactions, but, in exchange, we call for a non-cumulative procedure that taxes net earnings of financial investment portfolios, regardless of the number of intermediary transactions carried out, at rates equal to the average rate of the current tax system. Thus, if a Single Tax with a turnover rate of 3% raises revenue equal to 25% of GDP, the rate applicable to financial portfolio earnings should be the same 25%.
It is important to underscore this characteristic of the Single Tax, because the Federal Revenue, in its paper on the CPMF, strongly criticizes those who support exempting the financial markets, believing the exemption would be granted unaccompanied by specific taxation of that sector. This is obvious disinformation by the paper’s author, who states that such an exemption would “privilege a class of individuals, precisely the most fortunate, to the detriment of the remainder of the population subject to the CPMF.”
As for the fear of the Federal Revenue that the taxation method for financial investments proposed by Single Tax supporters “would demand extremely complex and costly operational control”, it is a surprising statement in view of the conclusions drawn by the critics themselves who, in another section of the paper, demonstrate convincingly that the electronic age and the progress in digital technology are capable of supporting a tax system that is based on electronic impulses, simply, cheaply, and efficiently. In other words, it would not be recommendable to give in on a correct conceptual principle merely because of presumed operational difficulties.
The second aspect of the CPMF strongly criticized by the Central Bank has to do with the allegation that as its nominal rate increases, its base of incidence is gradually eroded.
Initially, it is important to admit that any tax suffers from this effect. The higher the tax’s nominal rate, the greater is the stimulus to evade it. It is also expected that the strength of this effect tends to accelerate as the nominal tax rate increases.
Concerning this aspect, cumulative taxes such as the CPMF have some clear advantages. Tax base erosion occurs mainly as a function of marginal tax rates. In the case of value-added taxes, which are imposed on a smaller tax base (value-added at each production phase), the rates required to reach a given level of revenue are higher than those required by a cumulative tax, which is imposed on a broader base (gross value of sales). Furthermore, VATs have equal average and marginal rates, whereas in cumulative taxes the average rate is always higher than the marginal rate. Having said this, it is easy to conclude that the impact of self-erosion on the tax base may be stronger in VATs than in turnover taxes.
In the case of the CPMF, a measure of the tax base erosion that the Central Bank claims to have taken place in Brazil must be searched in the growth of bank disintermediation, in the drop in bank deposits, and in the concomitant expansion of the use of paper currency, to the detriment of fiduciary and other forms of currency such as checks, credit cards, electronic transfers etc. In other words, for the Central Bank’s allegation to be true, the public must have reduced its use of banking institutions, making increasing use of paper currency.
The data, however, do not support this statement. TABLE 20 shows that, following the fast drop in inflation after the Real Plan in 1994, and with the introduction of bank transaction taxes (which supposedly would have strongly increased preference for paper currency), indicators of preference for paper currency showed significant differences compared to earlier levels, albeit remaining at levels significantly lower than seen in other countries. Cash deposits in the banking system have been increasing in proportion to GDP, and the public’s preference for paper currency has remained practically constant vis-à-vis bank deposits.
Lastly, the evidence used by the Central Bank to argue against the CPMF, based on international experience, is not theoretically comparable to Brazil’s experience. The conditions for a well-functioning bank transaction tax do not exist in any other economy. Only Brazil satisfies the basic prerequisites conducive to the correct application of a bank transaction tax, as shown in other sections of this text. Thus, other countries’ experience with bank transaction tax are weak indicators of what could happen in Brazil, and which, from a conceptual point of view, turns any comparison into a totally speculative exercise. In other words, the coeteris paribus conditions for a correct comparison of operational efficiency across countries are not present.
TABLE 20
Concerning the alleged ill-effects the CPMF might have caused in Brazil’s stock markets, the Federal Revenue paper satisfactorily demonstrated the lack of a causal nexus between the CPMF and the drop in domestic trade volume. In fact, the creation of ADRs (American Depositary Receipts), which are surrogates for Brazilian stocks used in American stock trading, bears primary responsibility for the migration of such transactions to the U.S. market. The same occurred, as that paper demonstrated, in Argentina, Chile, and Mexico, whose domestic stock trade virtually disappeared (in Mexico, it dropped from US$ 300 million per day to less than US$ 30 million per day), even though there was no cumulative tax on stock market transactions in any of those countries. Actually, capital seeks greater liquidity such as found in US markets. For foreign investors, the use of ADRs reduces the risk associated with fluctuations in the rate of exchange. Thus, in Brazil, there is a clear causal relationship between stock trade migration abroad and the creation of ADRs, but not between migration and the CPMF. However, the Central Bank’s model of analysis ignores this causal nexus.
Summing up, the Central Bank’s paper is superficial, it mistakenly specifies the econometric models, and it omits variables and causal relationships that could significantly change its findings. Furthermore, it points solely to the costs and disadvantages of the CPMF, such as raising interest rates and its negative impact on the financial markets, but completely ignores its virtues, such as the elimination of tax evasion, the lowering of administrative costs to the public sector, and the reduction in corruption that goes hand in hand with non-declaratory, electronic taxes.
The other paper by the Central Bank also shows surprising conceptual and statistical weaknesses. It reveals the clear intention to demonstrate, by means of an illusorily methodological sophistication, something which cannot be easily proven, namely that the CPMF has caused significant financial disintermediation in Brazil.
The previously mentioned paper authored by the Federal Revenue states that, “the criticism linked to financial disintermediation can easily be refuted, since agents did not stop performing financial transactions as a result of the CPMF and the Brazilian banking system continues to operate normally.”
The Central Bank paper intends to demonstrate the undesirable impacts of the CPMF on financial markets. Thus, it claims that the CPMF erodes its own tax base and that it has been responsible for the reduction in the number of checks used in the economy (remonetarizing the economy); that the CPMF displaced savings deposits in favor of investment funds, and that it increased the banking spread.
The CPMF should not, indeed, be levied on the financial, credit, and capital markets. If the Government had correctly implemented the original Single Tax proposal, it would not have imposed the CPMF on such markets. Nevertheless, it is imperative that we point out the imprecision and technical weaknesses contained in the Central Bank studies, as they attempt to impute faults and distortions to the CPMF without solid empirical foundation. Rather than being scientific, the paper reflects misconceptions and prejudices.
To impute to the CPMF the decline in the number of checks issued is, at best, a gross mistake. Rather, such decline is part of an ongoing trend that occurred even during periods when the CPMF rates remained constant.
According to the Federal Revenue, the paper is misleading “because the model fails to consider the true variables that cause the reduction in the use of checks.” It states that “even the Brazilian System of Payments (an innovative and path breaking real-time and on-line system of transfers of bank reserves) will further stimulate real-time digital transactions, which means that the Central Bank’s policy will also seek to discourage the use of checks as a means of payment, since they are obviously not adapted to the digital economy.” Likewise, banks discourage the use of paper checks, either through charging high service fees, such as for use of checks, or through emphasizing the greater safety and reduced operational costs of electronic transactions. Therefore, the assertion that the CPMF is responsible for the drop in the use of checks is totally unfounded.
Furthermore, the Central Bank’s argument states that the CPMF, by taxing bank transactions, could stimulate the use of paper currency and the re-monetization of the economy. In addition to the fact that this hypothesis has not been confirmed, as we have seen above, this phenomenon is not accurately measured by the number of checks issued, as done in the Central Bank paper, but rather by the value of the checks issued. Because the use of checks carries an increasing per unit service charge, a more rational use of this payment instrument would imply that the average value of cleared checks would have increased. Even with a smaller number of checks, the value of transactions may have increased. In fact, as seen in TABLE 21, the value of checks cleared has only begun to drop significantly since 2003, with the development of internet banking and the growth of debit cards, showing no relation with the introduction of the CPMF in 1997.
TABLE 21
But the Central Bank’s attempts to criticize the CPMF are mistaken not only on conceptual grounds, but also on the econometric models and premises adopted. In addition to the misleading specification of the models (using the number rather than value of checks as the dependent variable in the regressions), the results are not strongly significant. Most of the estimated coefficients are not significantly different from zero. The same problems are found in the remainder of the paper in question: coefficients with no statistical significance and questionable conceptual models. Not to mention a contradiction found in one paper relative to the results reported in the other.
The Central Bank’s Discussion Paper No. 21 states that the base of the CPMF shows high elasticity with respect to the tax rate applied. This would explain, according to its author, the high dead-weight losses associated with it. On the other hand, in Discussion Paper No. 23 the claim is made that “the revenue base of the CPMF is inelastic relative to variations in its rate…” Surprisingly however, and though contradictory in the causal relationships claimed to be found, both studies were unanimous in criticizing the CPMF!
The inconsistencies found in these papers go so far as to claim that the growth of money supply as measured by M1, which in Brazil is basically the balance of cash deposits, increased because “checking account withdrawals and deposits for investment in extremely short-term funds are penalized by the introduction of this tax”. The truth lies elsewhere. It is the newly conquered monetary stability that makes unnecessary the high turnover of funds that marked Brazil’s hyperinflationary period. Furthermore, the paper calls irrational the behavior of an investor that accumulates cash deposits in order to avoid the 0.38% of the CPMF, but accepts the loss of monthly yield of more than 1% by leaving his funds idle in bank accounts. The Central Bank ignores the opportunity cost of cash deposit balances.
The same analytic superficiality and statistical weakness can be found in other correlations presented by the Central Bank. To say that “the CPMF might be inducing migration of savings account deposits to short term investment funds” is a claim completely devoid of causal nexus. The migration of funds that follows a transition from hyperinflation to stability is an obvious truism, and has little to do with the CPMF.
As the Federal Revenue states “the fact that two variables tend to show opposing tendencies does not necessarily mean that a direct or indirect relationship exists between them. Both can be influenced by other variables that explain the strong mathematical relationship indicated by the correlation coefficient.” The paper also states that “the main advantage of financial investment funds in relation to savings deposits is due to the following factors: greater individual access to the capital market; greater yield; better alternative for the small saver; and a reduction in risk exposure.” Thus, contrary to the Central Bank results, the inverse relationship between the use of the CPMF and diminishing balances in savings accounts is clearly a spurious correlation.
Finally, the Central Bank’s Discussion Paper No. 23 states that the CPMF significantly affects banking spreads. “It worsens the situation of borrowers, savers, and banks, because it increases the cost of loans to borrowers, reduces gains for savers, and decreases bank spreads”. The surprising aspect of this assertion is that it suggests the existence of a better tax alternative to the CPMF, which does not burden taxpayers, directly or indirectly. If such a tax does exist, the Central Bank should immediately make it public, as supporters of the Single Tax would certainly adopt this new and miraculous type of tax.
The authors demonstrate lack of knowledge of banking microeconomics. It is an oligopsony, with few credit suppliers and a large number of borrowers. Under these conditions it is fanciful to believe in the veracity of their conclusions as when they claim that “the borrower tends to demand a lower rate of interest in view of the need to pay not only the interest charged, but also the tax burden. On the other hand, the saver will demand, in addition to the usual return, an additional amount necessary to pay the tax.” Analysis of the elasticity of supply and demand in oligopsonic markets quickly shows how fanciful these assertions can be, since they imply an environment in which banks would be sandwiched between ambitious savers and powerful borrowers!
The Federal Revenue concludes its analysis of the Central Bank papers with a strong, though not surprising, statement. “Opposition to the CPMF in the financial markets is due to, in our opinion, the possibility that, through data generated by withholding the tax, the privacy of banking investors may be violated… the Federal Revenue agency will gain knowledge of all monetary transactions related to tax evasion schemes (unreported sales, drug dealing, bribes, corruption, etc.).”
Before concluding, it is important to address another controversial issue having to do with a bank transaction tax: its revenue productivity.
The studies published by the Central Bank mention the concept of the Laffer Curve, according to which tax rate increases lead to declining marginal tax revenue. They even suggest the possibility that tax revenue reaches a peak, after which, raising nominal tax rates imply negative marginal tax revenue, causing a decline in total revenue.
Within the limits in which the CPMF has been applied in Brazil, no evidence has yet turned up concerning the alleged drop in its marginal revenue. To the contrary, according to the International Monetary Fund, bank transaction taxes are recommended in situations of institutional weakness or erosion of the conventional tax systems, as can be seen in the following statement: “these new bank debit taxes have been imposed because the transactions on which they fall were viewed as a convenient and effective tax handle, against a background of weak tax administration and, typically, in the face of a difficult fiscal/revenue situation.” Thus, even if marginal revenue declines with higher rates, the CPMF is appropriate. Its notorious revenue raising potential is clearly above that obtained through worn down conventional self-assessed declaratory taxes.
According to the Federal Revenue, “the presence of a tax on bank debits in a stable tax system implies the existence of a highly productive tax, the minimization of total administrative costs (and, therefore, a higher net revenue [author’s insertion]), the guarantee that the underground economy is being taxed, and the adaptation of the tax system to the new reality of trade and electronic transactions.”
The Federal Revenue goes on to say that the CPMF is a “highly productive tax, with a high ratio of revenue per unit rate”. It quotes the IMF paper that says, “in the case of Brazil, in particular, a high revenue yield has been sustained over several years”. According to the IMF paper, Brazil’s CPMF productivity, measured by the proportional relationship of revenue/GDP relative to unit rates, remained practically stable during the period it was applied, having reached values of 4.14 in 1998. From then until 2007 the ration varied within narrow limits of 3.39 in 1999 and 3.68 in 2007. It has maintained high and sustained productivity over the years it has been in force.
This explains the growing interest other countries have shown in Brazil’s experience with a bank transaction tax, where it has been used in large scale over an extended period of time. In October 1999 the Parliamentarians for Global Action (PGA), with support and sponsorship of the United Nations, held a debate in New York at the UN headquarters, to discuss Brazil’s experience with bank transaction taxes. The meeting was attended by representatives of more than 40 countries. At that time I presented the paper transcribed in ANNEX III, which attempts to demonstrate the viability of this new type of tax, especially in economies that are still attempting to develop strong tax institutions and an ethical approach to taxation, as is the case in Brazil.
SETTING RATES FOR BANK TRANSACTION TAXES
Although the productivity of Brazil’s CPMF has remained robust and stable as its rate grew from its initial level of 0.20% to its final level of 0.38%, its adversaries insist on saying that it has reached its maximum tolerable level, warning that any increase will inevitably lead to stronger tax avoidance and evasion (even if difficult), and that, therefore, its base would shrink significantly.
The above-mentioned paper written by the Federal Revenue admits that, “the
Laffer curve effect exists not only for the CPMF, but for any tax: it is natural to expect that, for each percentage point of increase in the tax rate, marginal tax revenue will fall. Therein lies the art of fine tuning in tax policy, and from what we can see, the Brazilian experience has been successful…”
Actually, the rate capable of maximizing CPMF revenue is still far above 0.38%. This fact, if proven, would imply a significant support for the idea of imposing a tax such as the Single Tax on bank transactions.
Determining the point beyond which a rate increase would cause declining (or even negative) marginal revenue depends critically on the advantages and benefits that the modern banking system offers its clients. The only way to avoid tax incidence on bank transactions would be to cease using banks for clearing financial transactions. In other words, the incidence base of the CPMF will only suffer a decline if people stop using the banking system to make payments, and begin to replace bank fiduciary currency for outmoded paper currency. This would mean a remonetization of the economy.
The occurrence of this phenomenon will depend critically on the cost-benefit relationship between the tax savings derived from using paper currency (which is the same as the tax’s nominal rate) and the added transactional cost of doing away with bank services.
It is easy to verify that in integrated and globalized societies, remonetization of the economy is only a theoretical possibility. It would be inconceivable that in contemporary economies, where purchases and sales are made globally and with ever-increasing frequency, electronically, there would be even a remote possibility of receding to a system of person-to-person payments in paper currency. The costs would be astronomical and would mean the virtual destruction of the modern economy.
Likewise, how can anyone imagine that payments for all purchases and sales made in all the markets of the world could ever be made in cash? Would it make financial sense to anyone to make payments to suppliers and services at the cashier’s windows of the various commercial establishments, just to save a CPMF of 0.38% charged on the transaction? What would be the additional transaction cost of choosing to pay in cash?
Security, physical displacement, transportation, opportunity cost for time spent in manual payment, and many other reasons would imply a significantly higher marginal transactions cost compared to the tax saving. Such a choice would mean the rejection of all present-day progress and a return to economic pre-history. Therefore, it is difficult to imagine that this scenario would occur because of a reasonable CPMF rate increase.
But there still remains the matter of knowing what the tolerable rate ceiling would be for a bank transaction tax.
The theoretical answer would dictate that the ceiling rate would be the difference between the transactional cost of using paper currency and the corresponding costs of making payments through the banking system. That is, the rate would have to be equal to or greater than the maximum amount bank clients would be willing to pay in order to reduce the transactional costs if they use the banking system to make payments. As a mere theoretical exercise, one could assert that in a perfectly competitive economy, in which the price of a service equals its marginal benefit, the ceiling for the CPMF rate would be equal to the banking system’s participation in National Income.
In Brazil, during the inflationary period, the banking system reached 13% of GDP. More recently, it has decreased to about 6% of GDP. Thus, one can say that the rate at which the CPMF’s marginal revenue becomes zero, and then negative, is around 6%.
As evidence that the current CPMF rate is far removed from critical values for maintaining its current level of productivity, two important facts should be stressed.
First, is the growing importance of digital money and of electronic payments.
According to an article published in Information Week “in the United States, email payment systems now send money not only to friends and family, but also to online merchants, purchasers, and sellers, in a global environment.” In this system, clients send e-mails, as if they were checks from their electronic checkbooks. Most surprising, is the cost of these services. As can be verified on the website of one of these companies, PayPal (http://www.paypal.com), the service is free for remitters. For recipients, there is a fixed fee of 30 cents, plus 2.2% of the amount received. In the case of corporate market payments, the cost can be as high as 2.9% of the transaction amount. In some cases, the cost can be as much as 3.5%. Even with current fees “PayPal adds 50,000 new users to its customer base, every two days”. This is unequivocal evidence of the high value customers place on computerized banking services in the modern economies. It also shows convincingly the wide space for increasing CPMF rates and its enormous potential to become the basis of a tax model in the framework of the Single Tax.
Further evidence of the same phenomenon can be found in Brazil’s banking system. Fees charged by banks provide an assessment of the marginal utility of the services they supply.
A paper by ANEFAC (Associação Nacional dos Executivos de Finanças, Administração e Contabilidade [National Association of Finance, Management, and Accounting Executives] evaluates banking service costs in Brazil between March and May 2000. They are several times higher than the CPMF, in terms of an equivalent tax on bank transactions. TABLE 22 demonstrates that, in the case of corporations, banking services can cost as much as 1.43% of monthly invoiced sales. Because this concept can be considered equivalent to bank transactions (we are assuming that the velocity of bank circulation of corporate invoiced sales is equal to one; that is, corporation’s invoiced sales are deposited and withdrawn from the banking system only once), it is clear that no bank flight occurs, even if bank transactions are charged up to 1.43% merely to cover bank service fees.
For individuals, the evidence is equally convincing. TABLE 23 shows the equivalent monthly income needed to bring customer banking fees into equivalence with the CPMF, charged at 0.38%. As can be seen, the lower limit for monthly income must be R$ 17,116.00 and the upper limit, R$ 40,706.00. Because these income levels are higher than the 97th percentile of income distribution in Brazil, it is evident that wide space exists for raising CPMF rates before these would result in declining marginal revenue.
TABLE 22
It is clear, therefore, that there is compelling evidence that CPMF rates can be raised significantly without causing bank disintermediation or a remonetization of the economy. The evidence supports the belief that the Single Tax, based on a bank transaction tax, is totally viable, especially considering that rate increases in the transaction tax will occur concomitantly with the elimination of conventional taxes. Therefore, the tax burden would not increase. To this end, we should note that taxpayers see this as an acceptable option. Everardo Maciel said, “If we ask any
Brazilian taxpayer whether he prefers a 30% value-added tax regime, or a 2% cascading regime, I have no doubt what the answer would be.”
On the other hand, considering, as the Federal Revenue does, that this tax would not require fiscal bureaucracy (such as invoices, papers return forms, and other information usually required by traditional declaratory taxes), the cost-benefit relationship of this new tax model would be very favorable. “Collection of this tax occurs practically without any operational cost to the tax administration and to the taxpayer,” and would thus permit us to forecast the downsizing of the public bureaucracy as a result of reducing the tax burden to be extracted from the private sector.
THE IMPURITY OF VALUE-ADDED TAXES IN BRAZIL
Roberto Campos made extensive reference to the intriguing distinction drawn by Brazil’s business community between two types of cascade, as seen before. One, considered malignant, includes the hated CPMF, PIS, and Cofins. All criticism, whether fair or not, is leveled against them. The other, applauded unanimously by the business community, includes taxes that are considered laudable contributions made by Brazil to world tax practice: these are the Simple [simplified tax system for micro and small firms] and the presumed profits option for calculating corporate income tax. It is worth noting that the adoption of these two systems is entirely voluntary, and that, by making this choice, firms reduce their tax obligations and the bureaucracy involved in tax assessment. As such, these two modalities deserve extensive praise from business leaders, even though from a strictly technical standpoint the Simple and the presumed profits modalities are no less cumulative than are the CPMF or the Cofins.
It is worth noting that 93% of Brazilian companies have opted to use either the presumed profits or Simple modalities for calculating income tax. Companies that adopt these simplified tax collection procedures do not necessarily do so aiming exclusively at reducing their tax liabilities. Many prefer to pay more taxes, but to reduce compliance costs.
The presumed profits modality implies the acceptance of taxable margins that vary from 8% of sales to as much as 32%. Implicit taxable profit margins for the Simple modality can reach as much as 8.21 % of sales for micro businesses, and up to 17.42 % for small businesses. The implied profit margins are very high, compared to those reported by companies taxed under the real profit modality. What makes them choose an assessment procedure that implies cascading incidence, and often higher tax liabilities, is the much lower compliance costs implicit in these simplified systems.
Furthermore, the case for non-cumulativeness is weakened by the fact that even non-cumulative taxes have several forms of cumulative incidence.
A tax comes closer to being totally non-cumulative if legislation allows for generalized clearing of tax credits. In this case, the tax amount levied on all inputs (including permanent assets and usable/consumable inputs) can be claimed to compensate for tax liabilities. However, the ICMS, for instance, allows for tax credits on permanent assets, but does not allow tax credits on ‘consumed’ inputs, such as stationery or office telephone bills.
Furthermore, there are cases in which a firm’s administrative staff is not adequately trained, or equipped, to claim tax credits, thus turning a value-added tax into an effective turnover tax. This happens, for example, when small farmers purchase equipment, seeds, fertilizers, and insecticides, all taxed by the ICMS. Because they usually do not keep records of their sales and purchases, they are unable to claim credit for those transactions. Some States allow farmers to claim presumed credits based on their sales volume, but usually these compensations fall short of the their true value.
There are instances in which taxes are only partially non-cumulative because they only allow for physical credits. In this case, claims are limited to the amount of tax levied on acquisitions of inputs for production and sale, or alternatively, only for sale. In other words, tax credit is allowed only for inputs that enter and exit the production process, but not for permanent assets, such as machines and equipment. This is the case with the IPI (tax on industrial products).
Even the ICMS, considered to be a modern tax because of its value-added and therefore non-cumulative characteristics, can be heavily cumulative in its day-to-day operation. Every time the debit-credit chain is broken, it becomes cumulative. Nevertheless, in Brazil this seems to pass unnoticed. For example, the agricultural sector usually does not claim tax credits for the ICMS for lack of accounting procedures. Service sectors, not registered as contributors of the ICMS, are also liable for cumulative taxation since they cannot claim credits accumulated in purchases of taxed industrial inputs. The ISS (a municipal tax on services) is cumulative, as also would be the new IVV [Retail Sales Tax] on lodging and food which business community representatives want to include in the tax reform bill.
Even more amazing is that, in order to improve compliance, ICMS legislation has been undergoing changes that are totally cumulative. One example is the authorization for the food and restaurant sector in São Paulo to collect the valueadded tax as a percentage of gross sales, with no credits allowed. This turns it into a turnover tax. Due to high evasion and in the name of simplification, the government is adopting the same procedures in other sectors and for other value-added taxes, such as the non-cumulative PIS/Cofins; estimates of average value-added in each sector are imputed as bases for charging such taxes, which are collected as final payments with no credit being allowed in the other links of the production chain. Thus, Brazilian value-added taxes for operational reasons are becoming increasingly cumulative.
It is easy to see the ambiguity surrounding the debate on cascading taxes, if even the largest value-added tax in Brazil, the ICMS, is becoming ever more cumulative. In these cases, even hard line critics of cumulativeness ignore its cascading effect, provided it reduces the tax burden. However, anytime the cascade prevents evasion and implies a higher tax burden it is seen as highly distortionary.
The obvious conclusion is that criticism of cumulativeness is, in truth, an outcry of revolt against the high tax burden. It is a shame that this is not expressed clearly, which would bring greater transparency and rationality to the debate on tax reform.
Due to the regrettable involution of Brazilian tax system, the creation of a bank transaction tax was an innovation in which rests high hopes for greater tax efficiency. The CPMF/IPMF has become a very productive tax that is highly effective in preventing evasion. Nevertheless, the Brazilian tax system remains predominantly dependent on classical tax bases: income, circulation, property, payroll, and foreign trade. Thus, it remains dependent on declaratory taxes, which require extensive paper work. Taxpayers continue to self-assess and self-collect taxes using their own respective fiscal accounting procedures. Tax evasion lives on. The quality of the tax collection system remains poor. All a delinquent taxpayer must do to enjoy generous financial returns is not to comply with tax legislation, or else, to fiddle with his accounting procedures, knowing that his crimes have a low probability of being uncovered. Thus, corruption and growth of the underground economy continue to thrive in Brazil.
All in all, rejection of the bank transactions tax remains significant, even if it is capable of eliminating many of these distortions.
I recently received an e-mail from a friend who, indignant with the CPMF (the bank debit tax), said, “I pay taxes when I send money to my daughter who studies in another city, and she pays taxes again whenever she withdraws the money from the bank in order to use it. That makes no sense.”
The CPMF is a tax on the circulation of money. The existence of such a tax could be conceptually justified as being the payment for the supply of public services and for the public cost of making possible the circulation of money without physical handling. It is a tax on a social service that creates value, reduces transaction costs, and which society makes available through the banking services. Such a service would not be possible without institutions that guarantee its safety and reliability. Taxing the circulation of money is a cumulative process, but must not be confused with double taxation, which means multiple tax incidences on a single tax base.
But let us return to my friend’s line of questioning: he asks whether the CPMF – and, consequently, the Single Tax – are fair taxes.
An adequate response requires a meticulous cost-benefit analysis. At issue is not the fairness of a 0.38% tax on each bank transaction, but rather the possibility of its alternative being even more unfair to current tax payers, namely the resulting necessity of, for instance, increasing the current 27.5% income tax rate. Certainly, greater unfairness results from evasion made possible by declaratory taxes such as the income tax or the ICMS. Greater inequity lies in allowing multinational corporations to use transfer prices to remit their profits to foreign tax havens, thus avoiding collecting them in Brazil even though Brazilian public services are required in order to generate the very same profits that are sent abroad. It is not fair that tax rates have to be increased every passing year to compensate for tax revenue lost to increasingly sophisticated evasion mechanisms. For these reasons, in a proper costbenefit analysis, my friend should prefer to pay 0.38% – or even 3% if necessary – on his money orders to his daughter, to the alternative of collecting 27.5% out of his total wages or of paying 30% indirect tax on his grocery cart at the supermarket.
If there were a single tax, a single CPMF of, say, 3% or 4% on all bank transactions, almost all other taxes could be eliminated. There would be no tax avoidance, and this would certainly be fairer than the current system.
Unfortunately, political pressure coming from powerful lobbies commanded by the tax bureaucracy and by major tax evaders have managed to portray the CPMF as unfair, and the Single Tax as utopian and inefficient. But the truth lies elsewhere. Those who reject the Single Tax are those who will lose by not being able to practice tax evasion, or by not keeping control of the bureaucratic power with which the current declaratory system endows them.
If an oft-repeated lie eventually becomes the truth, then it is high time to question some of the allegations that have been made about the CPMF before they become universally accepted as true.
TAX COMPLIANCE COSTS: A NEW FIELD FOR RESEARCH
Conventional tax analysis has ignored an important criterion for evaluating the quality of tax collection models used around the world. Taxation studies begin with theoretical assumptions which are usually unsupported by economic reality, such as the presence of perfect competition, economic rationality, the absence of evasion, and negligible tax compliance costs. At the same time, analysts largely ignore the economic, cultural, ethical, moral, and operational environments in which tax collection takes place. An inevitable consequence is a conflict between intentions and results. Theoretical models are essential components in the construction of sound tax models. However, a disturbing fact is the failure of economists to realize that there is an abyss between their logical constructs and the reality of applied economics. Economists become prisoners to pure science, and the more innocent believe they can extend their “monoparadigmatic” prescriptions to reality .
“The broadly based neutral VAT found in textbooks is quite different from the VAT prevailing in most developing countries, and this difference results largely from administrative constraints: in developing countries tax administration is tax policy. Multiple VAT rates, zero-rating with refunds and numerous exemptions of specified goods can be accommodated only at high administrative and compliance costs”.
A recent study conducted in Brazil by Aldo V. Bertolucci fills a significant gap in the study of taxation, and inaugurated in Brazil a new area of study and research– the analysis of tax compliance costs – which is also relatively new in the world. One of its most important mentors is Professor Cedric Sandford of the University of Bath, England. This field of tax study first appeared in 1988 at the International Fiscal Association Conference in Rio de Janeiro, followed by two congresses on the Cost of Compliance at Oxford (1994) and Sydney (2000).
According to Professor Cedric Sandford, politicians, tax administrators, and economists have neglected the administrative and operational costs of taxation. These costs should be taken into consideration in tax policy analysis, in addition to the usual considerations regarding equity, neutrality, and simplicity. In retrospect, Professor Sandford stated, “following Adam Smith, no one else referred to compliance costs (with the honored exception of McCulloch in his Treatise on Taxation, published in 1845), until 1935, when the first attempt was made to measure them. However, the author stated that it was not until the end of the 20th Century that the topic was given importance, at the Rio de Janeiro conference in
1988.”174
At the Oxford Congress in 1994, Professor Cedric Sandford listed reasons for the growing interest in tax costs:175
1. Compliance and administrative costs are high and they reduce international competitiveness;
2. Compliance costs have undesirable redistributive effects, are highly regressive, and severely burden small businesses;
3. High compliance costs create resentment and stimulate tax avoidance;
4. The high costs generated by the creation of VATs in several countries have led to protests and dissatisfaction on the part of small business;
5. The importance of deregulation in order to unburden small business;
6. The need to begin considering the taxpayer as a client and treating taxpayers in a friendlier manner;
7. In the early 1980s, some governments reduced their administrative costs, shifting them onto the taxpayer and increasing compliance costs; they soon discovered that the social tax cost had increased in their economy as a whole.
Certainly, research in this area will open new horizons in tax studies, broadening the list of critical variants used in evaluating, reforming, and planning tax systems throughout the world. These fields of study and research will at once enrich the debate and partially divert the focus of economic policymakers’ attention from where it is today, biased by the formalistic approach of economists, toward a position of greater equilibrium between theoretical-conceptual considerations and practicaloperational experience. Economists must talk to tax administrators, and vice-versa.
Aldo Bertolucci has surveyed stock companies in Brazil, and gathered valuable information on their compliance costs.
Bertolucci says, that “compliance costs of taxation correspond to the resources
but almost nothing has been written about how to administer the receipt and control of revenue and of taxpayers”.
spent by a taxpayer to comply with tax legislation. Tax statements and reports required by federal, state, and municipal governments, filling of forms for federal revenue agencies, inclusions and exclusions defined by tax law, meeting auditing requirements and changes in legislation, lawsuits, as well as administrative and judicial processes…” represent a small portion of the total costs of taxation, because these are merely the monetary costs borne by companies in meeting their tax obligations. Other costs must be added to these, such as public operational and administrative costs borne by the three levels of government (federal, state, and municipal) and by their three branches (executive, legislative, and judiciary). One must also add the opportunity cost of time as well as the psychological costs imposed on the taxpayer, in addition to the imputed costs implied by economic distortions and by the loss of allocative and distributive efficiency introduced by taxes, as ILLUSTRATION 6 indicates.
ILLUSTRATION 6
Bertolucci’s findings are dramatic. The average total value of compliance costs to Brazilian stock companies accounts for 0.32 % of their gross income. In smaller companies, with annual sales of up to R$ 100 million, the cost is 1.66 % of their gross income. For all stock companies this cost reaches the equivalent of 0.75 % of GDP. Taking as reference the compliance costs of smaller stock companies alone, they represent 5.82 % of GDP, as can be seen in the TABLE 24.
This study was based on compliance costs for publicly held stock companies that are members of the Brazilian Association of Publicly Held Companies (Abrasca). The breakdown of their compliance costs, according to Bertolucci’s research, is found in ANNEX II. Such publicly held companies are usually large firms and, therefore, Aldo Bertolucci’s findings surely underestimate the overall compliance costs for all of Brazilian companies, given that tax costs are highly regressive in relation to sales volume.
TABLE 24
The size classification used in the survey considered as “small businesses” those companies with annual sales up to R$ 100 million. According to the Federal Revenue, 72% of firms that pay the PIS (a kind of social security contribution), are registered under the Simple method of tax calculation (requiring, therefore, maximum annual sales of R$ 1.2 million), and 21% chose to report profits under the “presumed profits” option (with maximum annual sales of R$ 24 million). These data indicate that the publicly held stock companies surveyed are large firms, at the top of the pyramid, and they certainly represent less than 1% of Brazilian companies.
It can thus be concluded that the overwhelming majority of Brazilian companies incur compliance costs that are higher than the corresponding 5.82 % borne by smaller Brazilian stock companies.
To calculate the overall cost of Brazil’s tax system, the administrative costs of tax collection to the government must be added to compliance costs borne by private firms and families. In centralized countries, which usually have simpler administrative structures, the ratio between public administrative costs and private compliance costs ranges from 1:2 to 1:4. Brazil is a federative republic, and has, therefore, an administrative structure that is more complex, with more decentralized taxation. Thus, the ratio can be conservatively estimated to be 1:3. It is easy to conclude that overall operational tax costs in Brazil are at least 7% of GDP. Nevertheless, these estimates should be interpreted cautiously due to the lack of detailed empirical studies on the subject.
It is worth noting that international research indicates a strongly regressive relationship between corporate gross sales and operational tax costs. The Annals of the International Fiscal Association Congress held in Rio de Janeiro in 1988, point to this phenomenon as one of the most significant conclusions of research done in Canada and the United Kingdom. This is a source of great competitive disadvantage for smaller companies.
Thus, despite that fact that operational tax costs in relation to average gross sales of domestic companies should be at levels between 1 and 2% of GDP, for most micro, small, and medium businesses – which account for 97% of Brazilian companies – operational tax costs and obligations take a hefty slice of production costs, over 7% of their value-added.
ARGENTINA’S USE OF THE BANK TRANSACTION TAX (1984-1992)
One often-heard criticism of bank transaction taxes has to do with its application in Argentina in 1984. The allegation is that the use of a bank debit tax in Argentina was an absolute failure. It is claimed that such experience left a mark in popular imagination with stories about intense banking disintermediation, which have become folklore in the diatribe against cumulativeness.
The truth is that Argentina’s unsuccessful experience in the 1980s had nothing to do with banking disintermediation, but rather with misguided economic policies adopted during that period.
Argentina’s bank debit tax went through several phases. Initially, it was a lowrevenue provisional tax. But it became an important component of the fiscal adjustment performed in that economy until its extinction in July 1992. Minister Cavallo, who raised the tax’s rate to 1.2%, attributed to the tax a fundamentally important role in his economic stabilization policy. The bank transactions tax raised US$ 1.8 billion, or 1.27% of GDP. It exceeded all other taxes charged in Argentina, except for the value-added tax (US$ 7.2 billion) and the fuel tax (US$ 2.7 billion).
The bank transactions tax was extinguished exclusively because of its incompatibility with the traditional tax model that was later implemented in that country. In fact, the transaction tax does not fit in with traditional tax structures. As Robert Campos says, “use of the bank transaction tax would only be revolutionary if it were the only tax and not an additional one.” 179 In the 1980’s, the priority of the Argentine government was focused on implementing the value-added tax (VAT). Argentina made rapid advances towards it, albeit with immense bureaucratic costs and a repressive atmosphere that bordered on fiscal fascism.
Critics of the transaction tax claim that Argentina’s tax on bank debits was the cause of heavy bank disintermediation. The increase in its rates apparently motivated a significant fall in bank transactions and, consequently, increased cash transactions (in dollars or in local currency). It also allegedly motivated higher transaction costs and losses of competitiveness by banks and economic agents in general. Thus, the critics hold, eliminating that tax was an imposition of good sense, and Argentina’s experience would recommend against implementing it in Brazil.
Such a chain of events, however, is spurious for the reasons that follow.
Brazil possesses structural conditions that are more favorable to the use of transaction taxes than Argentina’s. Even in its initial phase, when the transactions tax rate was 0.1% or 0.2% and, therefore, no attempt was made to avoid the tax, the ratio bank transactions/GDP was around 2.5. In Brazil this ratio is much higher, approximately 4, according to CPMF revenue data. In other words, banks in Brazil are used much more intensively than in Argentina. In fact, checks were little used there. They still are not used by individuals or by commerce. The banking system was minimally computerized and there was no national clearinghouse, as there is in Brazil. Transaction costs are high and checks carry little credibility as a form of payment.
Furthermore, imperfect regulation of Argentina’s tax on bank debits allowed for the corrosion of its base of incidence. Only checks were taxed, while other types of bank payments were exempt, such as collection accounts (cuentas de recaudación), transfers among accounts, term deposits, and third-party checks. There were differentiated rates and a large number of exemptions and waivers. These deviations were gradually eliminated, but tax avoidance was heavy during most of the life of the tax, drawing bank transactions/GDP ratio down to about 1.2 in 1991.
It is worth mentioning that this drop was primarily due to factors other than those related to the tax itself. From 1988 through 1991, Argentina suffered enormous economic instability and two hyperinflationary surges. In this period, cash deposits yielded highly negative returns, especially since interest rates were fixed by the government, and caused savings deposits (not taxed) to migrate to informal and unregulated overnight markets.
These illegal markets were managed in ways similar to black-market lotteries, known in Brazil as “jogo do bicho”, which function on strict confidence. Individuals also converted their earnings into dollars, with up to 4% discount, a clear demonstration of the loss of competitiveness of bank savings accounts relative to those informal deposits. Under these circumstances, there is no way to rightfully attribute bank avoidance to the tax on bank debits.
TABLE 25
Argentina’s experience teaches us a three-part lesson. First, a bank transactions
tax requires competent regulation to work properly. Secondly, Brazil has the structural conditions that allow us to predict that a bank transactions tax can be a successful experiment, as indeed it has turned out to be. Thirdly, it is a streamlined tax with low costs (as acknowledged by Argentina’s bankers themselves) that did not cause a negative reaction among economic agents.